Розтягнутий стержень деформується , як це зображено на рисунку 2.2, і змінює свої подовжні та поперечні розміри на відповідні величини та (при стиску було б та ).

Відносні деформації:

подовжня 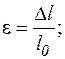(6)

поперечна (7)

Експериментально встановлено, що в межах пружних деформацій для кожного матеріалу зберігається постійне відношення

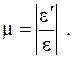(8)

Ця пружна константа називається коефіцієнтом поперечної деформації, або коефіцієнтом Пуассона.

Для будь-яких ізотропних матеріалів 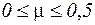. Для більшості конструкційних матеріалів 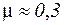; для пробки 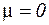; для гуми, рідини, а також при пластичних деформаціях твердих тіл можна прийняти .

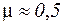Експерименти свідчать, що при навантаженні у відповідних межах для більшості матеріалів можна прийняти:

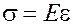. (9)

Ця залежність має назву закон Гукаі формулюється таким чином:

Нормальні напруження прямо пропорційні лінійним деформаціям.

В формулі (5) 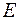– модуль подовжньої пружності або модуль пружності першого роду. Він характеризує властивості матеріалу опиратися пружному деформуванню, тобто чим більший модуль 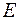, тим менше деформується матеріал. Оскільки 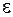– безрозмірна величина, то одиниці вимірювання 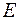ті ж, що і у 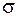, тобто Паскаль.

Для конструкційних сталей приймають 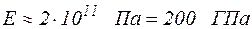, для міді .

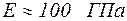Якщо в формулу (9) закону Гука підставити значення 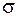та 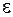згідно з (5) і (6), то отримаємо запис закону Гука для визначення абсолютних деформацій

. (10)

В цій формулі добуток називається жорсткістю при розтягу.

Слід відзначити, що формулою (10) можливо користуватися на ділянці стержня, в межах яко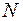ї і 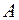залишаються постійними.

Розв'язання задачі