Тема 2: Розтяг і стиск.

План

1. Сутність деформації розтяг та стиск, внутрішні силові фактори при ній . Побудова епюр «N» та «σ» .

2. Поздовжні і поперечні деформації при розтязі (стиску). Закон Гука. Коефіцієнт поперечної деформації (Пунсона). Жорсткість перерізів жорсткість брусу.

3. Визначення осьових переміщень поперечних перерізів

4.Розв’язання задачі. Побудова епюр «N», «σ» і визначення абсолютного подовження

ЛІТЕРАТУРА ОСНОВНА

ЛІТЕРАТУРА ДОДАТКОВА

Студенти повинні знати: внутрішні силові фактори при розтязі, правила побудови епюр поздовжніх мил і нормальних напружень, вміти визначати осьове подоаження.

Студенти повинні вміти: будувати епюри та визначати осьове подовження.

1. Сутність деформації розтяг та стиск, внутрішні силові фактори при ній. Побудова епюр «N» та «σ»

Розтяг або стиск стержня викликається силами, що діють уздовж його осі (рис.2.1,а). При цьому в поперечних перерізах із шести внутрішніх силових факторів виникає тільки один — поздовжня (осьова) сила N, епюра якої наведена на рис.2.1,б. Осьова сила в перетині є рівнодіючою нормальних напруг, що виникають у кожній із точок перетину. Відсутність поперечних сил дає підставу припустити, що дотичні напруги в кожній точці поперечного перерізу дорівнюють нулю.

А яким чином ми будемо визначати напруги при розтязі та стиску ?

Розглянемо геометричну сторону завдання. При спостереженні деформації розтягу стержня, на поверхні якого нанесені лінії, перпендикулярні до осі брусу (рис.1,а), можна відзначити, що ці лінії, зміщуючись паралельно самим собі, залишаються прямими й перпендикулярними до осі бруса. Припускаючи, що зазначена картина переміщення перетинів має місце й усередині стержня, приходимо до гіпотези плоских перерізів: поперечні перерізи стержня, плоскі до деформації, залишаються плоскими й після неї, переміщуючись поступально уздовж осі стержня.

а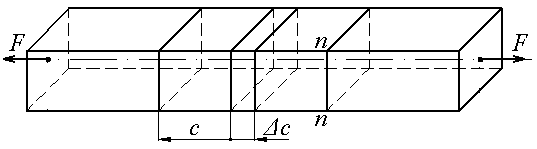
б
в

Рис.1. Поздовжня сила в перетині і її епюра

Розіб'ємо стержень на поздовжні (паралельні осі стрижня) елементи нескінченно малих поперечних перерізів і будемо надалі називати їх волокнами. На підставі гіпотези плоских перетинів варто укласти, що всі волокна подовжуються на ту саму величину і їхні відносні подовження 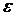однакові:

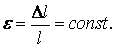
(1)

Це аналітичне вираження геометричної сторони завдання.

Фізична сторона розглянутого завдання полягає у встановленні залежності деформацій від напруг. При пружних деформаціях ця залежність підкоряється закону Гука:

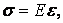
(2)

де Е — модуль пружності першого роду.

З огляду на сталість модуля пружності Е для однорідного ізотропного матеріалу, а також(1)і (2), знаходимо, що

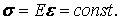
(3)

Підставляючи вираз (2.2) в (2.3), одержуємо

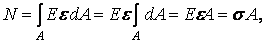
(4)

Звідки

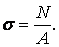
(5)

Знак напруги залежить від знака поздовжньої сили в розглянутому перетині. У випадку стиску напруги вважають від'ємними. Формула (5) справедлива лише для перетинів, досить віддалених від місць прикладення зосереджених навантажень.

Визначаючи напруги при розтягу, стиску й інших видах деформацій, широко користуються положенням, що носить назву принципу Сен-Венана: якщо тіло навантажується статично еквівалентними системами сил, тобто такими, у яких головний вектор і головний момент однакові, і при цьому розміри області додатка навантажень невеликі в порівнянні з розмірами тіла, то в перетинах, досить вилучених від місць додатка сил, напруги мало залежать від способу навантаження.

Загального теоретичного доказу принцип Сен-Венана не має, але його справедливість підтверджується численними теоретичними й експериментальними дослідженнями.

Пояснимо цей принцип на наступному прикладі. Той самий стрижень, закріплений верхнім кінцем, навантажується на вільному кінці статично еквівалентними навантаженнями, рівнодіючі яким виражаються величиною вектора F. Навантаження прикладені різними способами: а) у вигляді зосередженої осьової сили; б) у вигляді двох сил; в) у вигляді розподіленого навантаження. Дослідження показують, що у всіх випадках у поперечному перерізі, віддаленому на відстань, що перевищує в 1, 5-2 рази його поперечні розміри, напруги практично однакові. У перетинах же, розташованих близько від місця додатка сил, величина напруг і характер їхніх розподілів різні.

Поздовжні і поперечні деформації при розтязі стиску).Закон Гука. Коефіцієнт поперечної деформації (Пунсона). Жорсткість перерізів, жорсткість русу. Визначення осьових переміщень поперечних перерізів

Осьовим (центральним) розтягом або стиском брусу – називається такий простий вид навантаження, при якому єдиним внутрішнім силовим фактором у поперечному перерізі цього стержня є внутрішня поздовжня сила .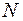

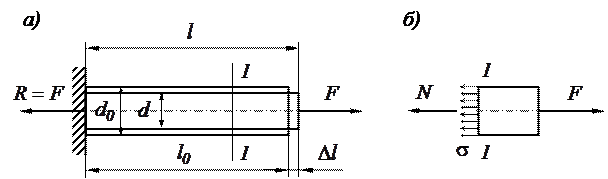Простіше за все цей вид навантаження можна реалізувати, якщо прикласти до стержня зовнішні сили 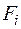, лінія дії котрих збігається з його віссю (рисунок 2.2 а).

Рисунок 2 Модель розтягу брусу

Для визначення внутрішньої подовжньої сили застосуємо метод перерізів (рисунок 2 б).

З умов рівноваги уявно відрізаної частини стержня отримаємо: .

У загальному випадку, коли зовнішніх сил декілька, маємо правило:

Подовжня сила 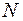у поперечному перерізі стержня чисельно дорівнює алгебраїчній сумі проекцій на вісь стержня зовнішніх сил, розташованих
з однієї сторони перерізу.

Правило знаків: 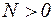, якщо вона розтягує (направлена від перерізу);

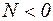, якщо вона стискає (направлена до перерізу).

У поперечних перерізах діють тільки рівномірно розподілені (гіпотеза Бернуллі) нормальні напруження σ, що можуть визначатися за формулою

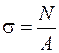, (5)

де 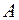– площа перерізу.