Основні гіпотези і припущення в опорі матеріалів.

Багаторічні експериментальні дослідження та досвід розрахунків на міцність дозволили фахівцям в додаток до розглянутих раніше гіпотез щодо матеріалу сформулювати кілька основних принципів, які є загальноприйнятими та спрощують розрахунки:

Принцип початкових розмірів. Малі деформації і переміщення деталі (споруди) не враховуються при складанні рівнянь рівноваги. Тобто деталь розглядається як недеформована, але тільки на етапі статичного аналізу.

Принцип суперпозиції або незалежності дії сил. Якщо деформації (напруження) змінюються пропорційно до навантажень (лінійність системи), то можна у довільному порядку додавати деформації (напруження), що виникли від дії окремих сил. Загальний деформований (напружений) стан деталі не залежить від порядку прикладання зовнішніх сил.

Принцип Сен-Венана. Якщо довільне навантаження прикладене в області, розмір 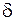якої малий у порівнянні з розмірами деталі, то деформований (напружений) стан у точках, віддалених від місця навантаження на 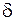чи більше, практично не залежить від конкретного способу прикладання навантаження. Таким чином, наприклад, розподілені сили, прикладені в малій області, можна замінити в розрахунковій схемі зосередженою рівнодіючою силою.

Про деякі інші припущення та гіпотези йдеться далі у відповідних розділах посібника.

Більшість реальних задач в галузі розрахунків на міцність є статично невизначеними що ускладнює розрахунки величин внутрішніх сил і напружень і обумовлює необхідність додаткового аналізу деформованого стану деталі. І навпаки, деформації не можуть бути розраховані окремо від напружень.

Розглянемо в загальних рисах основний універсальний метод, за допомогою якого принципово можливо розв’язати будь-які задачі механіки твердого деформівно́го тіла. Згідно з цим методом задача повинна розглядатися з трьох сторін (рисунок 1.3):

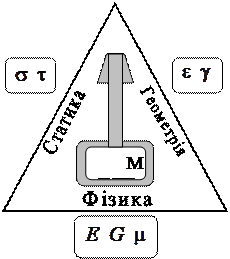Рисунок 3 – „Опорний сигнал” щодо основного методу
механіки твердого деформованого тіла (МТДТ)

Статична сторона задачі, де

· розглядаються – внутрішні силові фактори та напруження, ;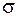

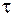· основна ідея– ідея рівноваги будь-якої уявно відокремленої частини деталі (конструкції);

· реалізація– у вигляді рівнянь рівноваги.

Геометрична сторона задачі, де

· розглядаються – переміщення та деформації , ;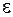

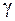· основна ідея– ідея узгодженості деформацій будь-яких суміжних частин деталі (конструкції);

· реалізація – у вигляді рівнянь сумісності деформацій.

Фізична сторона задачі, де

· розглядаються – деформівні́ властивості матеріалу, які характеризуються фізичними пружними константами, такими як модуль подовжньої пружності 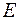, модуль зсуву 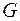, коефіцієнт Пуассона 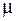(фізичний смисл цих величин ми будемо розглядати в подальшому);

· основна ідея– ідея взаємозалежності напружень і деформацій;

· реалізація – у вигляді рівнянь Гука або інших законів деформування, які зв’язують між собою напруження і деформації і до яких входять вищезгадані фізичні константи.

Статичні, геометричні та фізичні рівняння сукупно складають так звану розв’язувальну систему рівнянь, з якої принципово можливо визначити всі невідомі: напруження і деформації.

Рисунок 3 є так званим „опорним сигналом”, який за допомогою асоціацій, коротких підказок, абревіатур та ін. допомагає краще запам’ятати та зрозуміти суть питання (у нашому випадку суть основного методу).

У подальших розділах посібника, при вивченні розтягу, згину, кручення брусу, ми неодноразово будемо користуватися цим основним методом МТДТ.

Питання для самоконтролю

1. Визначити основні завдання курсу опору матеріалів.

2. Що розуміють під міцністю, жорсткістю і стійкістю матеріалів?

3. Як в опорі матеріалів класифікуються зовнішні сили?

4. Дати визначення внутрішніх сил. Чим відрізняється поняття внутрішніх сил у курсі опору матеріалів від означення цих сил у фі­зиці? Які ви знаєте внутрішні силові фактори?

5. Розкажіть про призначення і сутність методу перерізів.

6. Що таке епюра внутрішніх силових факторів? Розкажіть правила побудови епюр.

7. Які гіпотези використовують у курсі опору матеріалів?

8. Що таке деформація тіла? Які види деформацій вам відомі?

9. Що таке напруження в точці перерізу тіла? Її одиниці.

Заняття № 35