Мобильность лопастной линии аммоноидей

Процесс возникновения новых форм в ходе эволюции весьма необычен, поэтому ему трудно подобрать какую‑то аналогию из нашей практической жизни. Обратимся к миру фантазии. Вообразим, что мы летим в звездолете, и расстояние, которое предстоит преодолеть, столь велико, что на это путешествие должна уйти почти вся жизнь. Самое неприятное в этих условиях – непредвиденные задержки, но, к сожалению, именно с ними нам и пришлось столкнуться.

Вопреки ожиданиям, межзвездное пространство оказалось неоднородным, и мы то и дело попадаем в зоны с аномальными, заранее непредсказуемыми свойствами. Выяснилось, что пройти эти зоны можно лишь при условии изменения кораблем своей формы, т. е. перед входом в каждую новую аномальную область пространства мы должны перестраивать оболочку звездолета, придавая ей вид (в зависимости от «требований среды») то диска, то спирали, то шара и т. д. На подобные операции требуется какое‑то время, поэтому успех всего путешествия попадает в зависимость от скорости, с которой мы способны изменить форму корабля. Эту скорость мы могли бы назвать мобильностью оболочки; очевидно, что именно она и является главным (ведущим) свойством, от которого зависят наши шансы дожить до конца пути.

Оболочка корабля, конечно же, состоит из разнородных частей (компонентов), которые различаются по назначению, конструкции, материалу, а стало быть, и по мобильности. Если функция данных частей допускает несколько конструктивных решений, то для ускорения полета естественно выбрать те, которые позволят перестроить корабль за минимальное время. При этом свои основные усилия мы сосредоточим на мобилизации наименее пластичных компонентов. Ясно, что после серии таких реконструкций мы снабдим звездолет оболочкой, все компоненты которой будут отвечать принципу максимальной мобильности.

Теперь перейдем к эволюции аммоноидей. Сначала отметим, что ведущим признаком, изменение которого позволяет виду покинуть старую экологическую нишу или захватить новую, является размер особей, который для аммоноидей удобно оценивать по величине радиуса раковины. Мобильность сутуры, по существу, является только одной из компонент мобильности размера раковины. Другими ее компонентами могут выступать мобильности таких признаков раковины, как толщина стенки, число поперечных перегородок, наружная скульптура и др.

Сдвиг величины логарифма радиуса раковины (ΔlnR ), сопровождающий видообразование, очевидно, возникает как результат серии фиксаций благоприятных мутаций. Скорость фиксации каждой такой мутации определяется при прочих равных условиях селективным выигрышем, который получает ее носитель (см. (3.32)). Пусть мы имеем два класса мутаций, любая из которых укрепляет стенку раковины в одинаковой степени, но мутации первого класса утяжеляют раковину, а мутации второго класса – нет. Очевидно, что движущий отбор отдаст предпочтение мутациям второго класса из‑за более высокого коэффициента селекции. Наиболее эффективный способ упрочить раковину, не изменяя массы (см. гл. 5), состоит в удлинении лопастной линии за счет увеличения числа ее изгибов, т. е. за счет повышения сложности.

Следовательно, виды аммоноидей с более сложной сутурой имеют больше шансов на филетическое выживание, когда среда «требует» изменения размеров раковины. Данное обстоятельство способно обусловить макроэволюционную тенденцию к повышению мобильности лопастной линии. Мы регистрируем эту тенденцию как постепенное увеличение в ходе исторического развития среднего значения и размаха видовых распределений по сложности сутуры аммоноидей. В конце концов мобилизующий отбор мог бы привести к снабжению каждого вида сверхгибкой лопастной линией, способной адекватно изменять степень своей изогнутости при любом требовании среды к изменению величины и прочности раковины.

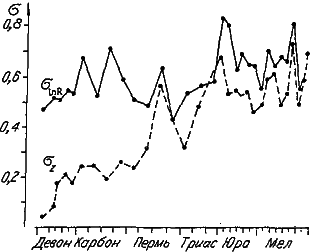
Рис. 30 . Динамика изменения среднеквадратического отклонения (сигмы) видовых распределений аммоноидей по размеру раковины σ_lnR и сложности лопастной линии σ_z.

Теперь попробуем оценить величину межвидовой изменчивости по сложности сутуры в филетической группе, где все виды обладают сверхгибкой лопастной линией. Площадь боковой поверхности раковины растет пропорционально квадрату ее радиуса и по тому же закону должна возрастать длина сверхгибкой сутуры (l_∞ ). В то же время длина контура поперечного среза раковинной трубки (l₀) пропорциональна ее радиусу (R ), поэтому отношение l_∞ /l₀ тоже должно быть пропорционально радиусу, т. е.

l_∞ /l₀ = kR , (6.3)

где k – коэффициент пропорциональности. В логарифмической форме равенство (6.3) преобразуется в

ln(l_∞ /l₀ ) = lnR + lnk . (6.4)

Заметим, что в левой части этого уравнения стоит сложность сверхгибкой сутуры, а член lnk в правой части – константа. Изменчивость константы равна нулю, поэтому изменчивость сложности сверхгибкой сутуры должна равняться изменчивости логарифма радиуса раковины. Выбрав в качестве меры межвидовой изменчивости сигму, для сверхгибкой сутуры должны иметь

σ_z = σ_lnR . <6.5>

Таким образом, в пределе, когда требования к прочности раковины стали бы полностью удовлетворяться изменением длины сутуры, межвидовая изменчивость по ее сложности сравнялась бы с межвидовой изменчивостью по логарифму радиуса.

Наши данные (рис. 30) показывают, что в ходе эволюции аммоноидей σ_z как бы стремится сравняться с σ_lnR, однако эта «цель» не достигается даже аммонитами юры и мела. По‑видимому, какая‑то часть требований среды к укреплению стенки раковины продолжала удовлетворяться за счет других средств. Тем не менее согласованное изменение сигмы обеих величин в течение последних 130 миллионов лет истории аммоноидей ярко демонстрирует, что технические возможности генетической системы, мобилизующей сутуру, фактически были доведены до предела.