Алгоритмы факторизации.

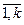Пусть n > 1. Требуется найти его разложение на простые сомножители , где p_i – простые числа (i = ), то есть факторизовать n.

Как было показано в Главе 1, с проблемой факторизации тесно связаны такие теоретико-числовые проблемы, как поиск квадратных корней по составному модулю (в том числе и проблема RSA), проблема распознавания квадратов и псевдоквадратов по модулю Блюма, проблема вычисления функции Эйлера. Было показано, что каждая из этих проблем не сложнее проблемы факторизации, а некоторые из проблем ей эквивалентны. Во всяком случае, решив задачу факторизации, дальнейшее решение каждой из этих проблем осуществляется за полиномиальное время.

Поэтому задача факторизации представляется столь важной, и количество разнообразных алгоритмов факторизации весьма велико. Конечно же, невозможно привести всевозможные алгоритмы в рамках одного параграфа ввиду не только их количества, но и сложности. Далее приведены некоторые алгоритмы факторизации, которые иллюстрируют основные направления в исследовании данного вопроса.

Прежде чем приступить к факторизации числа, необходимо учесть следующее:

1) Если n – четное число, то следует выделить из него все степени двойки. Такая операция является легкой, особенно если число n представлено в двоичной форме. Тогда выделение степеней двойки – это битовый сдвиг вправо до тех пор, пока в младшем бите не появится «1».

2) Проверка на простоту проще, чем факторизация, поэтому прежде чем начать факторизацию нечетного n, следует проверить его на простоту.

3) Следует проверить, не является ли n целочисленной степенью какого-либо числа (n = x^k). Такая задача решается вычислением 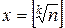для всех целых k 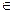[2,log₂n] (если n предварительно проверено на четность, то k 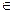[2,log₃ n]).

4) Следует рассмотреть задачу 2-факторизации (сплиттинга), или расщепления n=a∙b (1<a,b<n)

Далее для всех алгоритмов полагаем, что n – составное число, нечетное и не степень целого числа.

Все алгоритмы факторизации делятся на алгоритмы общего назначения, то есть такие алгоритмы, которые подходят для факторизации любого числа, и алгоритмы специального назначения, то есть алгоритмы, которые факторизуют числа определенного вида, например, числа, имеющие маленькие делители, или числа, имеющие только большие делители, или числа, свободные от квадратов и т.п.

На протяжении данного параграфа факторизуемое число будем обозначать n.