Кольца многочленов.

В предыдущей главе мы подробно рассмотрели кольца Z_m и поля Z^*_p , элементами которых являлись целые числа. Выяснили, что Z_p^* является циклической группой относительно умножения, а также заметили, что любое конечное поле размерности p изоморфно Z^*_p для подходящего p.

Рассмотрим произвольный многочлен степени k с коэффициентами из Z_m:

f(x) = a_kx^k + … + a₁x + a₀.

Степень многочлена будем обозначать как deg f(x).

В силу того, что Z_m – коммутативное кольцо, множество всех многочленов с коэффициентами из Z_m также образуют коммутативное кольцо Z_m[x] вместе с операциями сложения и умножения многочленов. Операция сложения многочленов f(x) = a_kx^k + … + a₁x + a₀ и g(x)=b_kx^k + … + b₁x+b₀ задается как

f(x)+g(x) = (a_k+b_k mod m) x^k + … + (a₁+b₁ mod m) x + (a₀+b₀ mod m),

умножение как

f(x)g(x) = (a_kb_k mod m) x^2k +(a_k-1b_k+a_kb_k-1 mod m)x^2k-1 … + (a₁b₀+a₀b₁ mod m) x + +(a₀b₀ mod m),

то есть как обычное сложение и умножение многочленов, но операции сложения и умножения коэффициентов производятся по модулю m.

Пример 1.

Рассмотрим Z₂[x]. Это множество состоит из всех многочленов с коэффициентами из {0,1}. Возьмем два многочлена из Z₂[x]:

f(x) = x⁴+x²+1,

g(x) = x⁴+x³+x+1.

Вычислим сумму и произведение этих многочленов.

f(x)+g(x) = (1+1 mod 2)x⁴ + (1+0 mod 2)x³ + (0+1 mod 2)x² + (1+0mod 2)x + + (1+1 mod 2) = x³+x²+x.

f(x)g(x) = (x⁴+x²+1)(x⁴+x³+x+1) = x⁸ + x⁷ + (2 mod 2)x⁵ + (2 mod 2) x⁴ + x⁶ + (2 mod 2) x³ + x² + x + 1 = x⁸ + x⁷ + x⁶ + x² + x + 1.

Многочлен из Z_m[x] называется неприводимым над Z_m, если его нельзя представить в виде произведения каких-либо двух многочленов из Z_m[x]. Понятие неприводимого многочлена в кольце многочленов эквивалентно понятию простого числа в кольце целых чисел.

Так же как и для кольца целых чисел, для колец полиномов справедлива

Теорема (о делении с остатком)

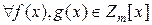
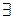единственная пара многочленов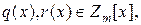

0 ≤ deg r(x) < deg g(x): f(x)=g(x)q(x)+r(x).

■

Пример 2.

Разделим многочлен f(x) =x⁷+x⁴+x²+1 на g(x) = x³+x+1 с остатком над Z₂[x].

Деление будем производить «в столбик».

_— x⁷+ x⁴+x²+1 │ x³+x+1

x⁷+ x⁵+x⁴ │x⁴+x²+1

_ x⁵ + x²+1

x⁵ +x³+x²

_ x³+ 1

x³+ x +1

x

Итак, f(x) = g(x)( x⁴+x²+1) +x.

В силу справедливости данной теоремы, над кольцом Z_m[x] можно определить теорию делимости и теорию сравнений, как и над Z.

Если существует многочлен h(x): f(x)=h(x)g(x), то говорят, что g(x) делит f(x) и пишут g(x)\f(x).

Если g₁(x) и g₂(x) имеют одинаковые остатки при делении на f(x), то говорят, что g₁(x) и g₂(x) сравнимы по модулю f(x) и пишут g₁(x)≡g₂(x) (mod f(x)).

Свойства, справедливые для сравнений над кольцом целых чисел, справедливы и для сравнений над кольцами многочленов.

3.2. Кольцо многочленов Z_p[x].

Рассмотрим более подробно кольцо многочленов Z_p[x], где p – простое число.

Справедлива

Теорема (о единственности разложения).

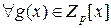, если g(x)≠0, существует единственное разложение g(x)=a·f₁(x)∙f₂(x)∙…∙f_n(x), где, f_i(x) – приведенные неприводимые (не обязательно различные) многочлены над Z_p[x] .

■

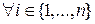При помощи алгоритма Евклида можно вычислить наибольший общий делитель двух многочленов. Справедлив и расширенный алгоритм Евклида для многочленов.

Пример.

Отыщем НОД(x⁵+x²+x+1, x³+x²+x+1) над Z₂[x]. Воспользуемся алгоритмом Евклида:

x⁵+x²+x+1=(x²+x)( x³+x²+x+1)+(x²+1)

x³+x²+x+1=(x+1)(x²+1)+0.

Ответ: НОД(x⁵+x²+x+1, x³+x²+x+1)= x²+1.