Метод пробных делений.
Этот метод является методом специального назначения и рекомендуется для отсеивания маленьких делителей на первом шаге. Если известно, что число не имеет малых делителей (например, модуль RSA), то этот метод не стоит применять.
Прежде чем приступать к факторизации числа этим методом, следует выделить все степени двойки и тройки.
Задается некая теоретическая граница B ≤ 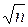 , которая задает максимальную величину испытываемых делителей и обусловливается доступным объемом памяти и вычислительными возможностями, а также некоторыми априорными сведениями о структуре числа n.
, которая задает максимальную величину испытываемых делителей и обусловливается доступным объемом памяти и вычислительными возможностями, а также некоторыми априорными сведениями о структуре числа n.
Если В невелико, то строим заранее таблицу простых чисел, меньших или равныхВ и проверяем делимость n на эти числа.
Иначе выбираем числа d1=5, d2=5+2=7, d3=d2+4=11, d5=d4+2, … , dk > B. (чередуем шаг +2 и +4 с тем, чтобы отсеять числа, кратные «2» и «3»).
Эти d1, … , dk являются возможными делителями n. Осуществляем пробные деления на di (i = 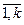 ). При этом действия осуществляются в следующем порядке:
). При этом действия осуществляются в следующем порядке:
Для каждого i:
Ш.1. Генерируем di.
Ш.2. Осуществляем пробное деление на di. Если di\n, то n=n/di и повторяем
Шаг 2. Если di не делит n, то идем на Шаг 3.
Ш.3. Уничтожаем di, освобождаем память.
Заметим, что все малые делители, выделенные вышеуказанным способом, будут простыми.
Метод Ферма.
Метод специального назначения, применяется для 2-факторизации, или сплиттинга.
Если n – нечетное составное число, не являющееся степенью целого числа, то этот метод находит целые числа x, y: n=x2—y2 . Тогда n=(x+y)(x—y).
Алгоритм:
Ш.1. Вычисляем x= 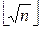 +1.
+1.
Ш.2. Если x= 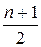 , то идем на Выход с сообщением «n – простое число».
, то идем на Выход с сообщением «n – простое число».
Ш.3. Вычисляем z=x2—n и y= 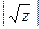 . Если y2=z, то идем на Выход, a=x+y, b=x—y.
. Если y2=z, то идем на Выход, a=x+y, b=x—y.
Ш.4. Вычисляем x=x+1. Идем на Шаг 2.
Выход: n=a·b.
Отметим, что делители a и b, получившиеся в результате 2-факторизации Ферма, в общем случае не являются простыми и требуют проверки на простоту и дальнейшей факторизации.
Дата добавления: 2015-11-28; просмотров: 4492;
