Метод квадратичного решета.
Пусть n – число, которое надо факторизовать. Как и метод Ферма, данный метод ищет целые числа x, y: n=x2—y2, но подход к поиску несколько иной. Поиск числа x осуществляется не среди всех чисел подходящего размера. Перед началом перебора производится отсев некоторых чисел.
Принцип отсева вытекает из следующих рассуждений: Возьмем небольшое число m и рассмотрим полную систему вычетов Zm={0, 1, 2, … ,m—1}. Среди чисел из Zm некоторые числа являются квадратами (то есть квадратичными вычетами), а другие не являются. Если m – простое число, то квадратов столько же, сколько неквадратов. Если m – составное, то квадратов несколько меньше. В общем случае,
P(s 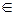 Q(m)) ≤
Q(m)) ≤ 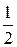 .
.
Если число не является квадратичным вычетом по какому-то модулю m, то оно не является квадратом в Z, поэтому число y2 следует искать среди тех чисел, которые являются квадратами в Zm.
В методе квадратичного решета берут несколько небольших попарно простых модулей m1, m2, … , mk. Для каждого такого модуля составляют квадратичное решето (двоичный вектор Sm) следующим образом:
Для каждого x 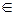 Zm вычисляют x2 mod m и z=(x2—n) mod m. Если z является квадратом по модулю m, то Sm(x)=1, иначе Sm(x)=0. Проверка того, является ли z квадратом по модулю m, производится путем сверки с вычисленными x2 mod m.
Zm вычисляют x2 mod m и z=(x2—n) mod m. Если z является квадратом по модулю m, то Sm(x)=1, иначе Sm(x)=0. Проверка того, является ли z квадратом по модулю m, производится путем сверки с вычисленными x2 mod m.
| X | … | m–1 | |||
| x2mod m | 22 mod m | … | (m–1)2mod m | ||
| z=x2–n mod m | z2 | … | zm—1 |
После того, как все решёта построены, начинается отсев кандидатов x. Решёта накладываются на последовательность чисел x от 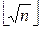 +1 до
+1 до 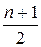 . Те числа, на которые наложился «0» хотя бы одного решета, отсеиваются. После отсева остается достаточно небольшое количество чисел – кандидатов в x. Для каждого такого числа вычисляется x2, z= x2–n и y=
. Те числа, на которые наложился «0» хотя бы одного решета, отсеиваются. После отсева остается достаточно небольшое количество чисел – кандидатов в x. Для каждого такого числа вычисляется x2, z= x2–n и y= 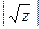 . Если y2=z, то числа a=x+y, b=x—y являются делителями числа n.
. Если y2=z, то числа a=x+y, b=x—y являются делителями числа n.
Пример:
n=279.
Построим решёта по модулям 4, 5 и 7:
| x | ||||
| x2mod 4 | ||||
| Z=x2–279 mod 4 | ||||
| S4 |
| x | |||||
| x2mod 5 | |||||
| z=x2–279 mod 5 | |||||
| S5 |
| x | |||||||
| x2mod 7 | |||||||
| z=x2–279 mod 7 | |||||||
| S7 |
Теперь, когда мы построили три решета, наложим их на последовательность чисел от 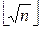 +1=17 до
+1=17 до 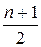 =140.
=140.
Поскольку 17 mod 4 = 1, то наложение решета S4 начнем с S4(1),
17 mod 5 = 2, то наложение решета S5 начнем с S5(2),
17 mod 7 = 3, то наложение решета S7 начнем с S7(3).
| x | ||||||||||||||||||
| S4 | ||||||||||||||||||
| S5 | ||||||||||||||||||
| S7 |
Среди чисел от 17 до 34 остались 20, 22, 28,
Проверим их:
x=20, x2=400, z=x2—n=121, y= 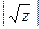 =11, y2=121=z.
=11, y2=121=z.
Тогда a=x+y=31, b=x—y=9.
Ответ: 279=31·9.
Ро-метод Полларда.
Ро-метод Полларда – метод специального назначения для поиска малых делителей.
Пусть n – число, которое требуется факторизовать, и f(x) – случайный полином над Zn. Возьмем x0 – случайное число из Zn и построим последовательность x1, x2,…., xk, … по правилу xi+1=f(xi), i=0, 1, …. Поскольку Zn – конечное множество, то рано или поздно в последовательности возникнет xs+i=xi, s<n. То есть последовательность x1, x2,… войдет в цикл периодом s.
Замечание: среднее ожидаемое величины периода последовательности, построенной выше, есть E(s)= 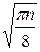 .
.
Пусть p – простой делитель числа n, и в последовательности, построенной выше, нашлись числа xi, xj: xi≡xj (mod p), xi  xj (mod n).
xj (mod n).
Тогда p\НОД(xi—xj,n), n не делит НОД(xi—xj,n), а значит НОД(xi—xj,n) является нетривиальным делителем n.
Ро-метод Флойда использует функцию f(x)=x2+1 mod n, а для поиска чисел xi, xj применяет метод Флойда поиска периода последовательности.
Метод Флойда поиска периода последовательности:
Вычисляем x2=f(x1). По паре (x1, x2) вычисляем пару (x2=f(x1), x4=f(f(x2))) и т. д., по паре (xi, x2i) вычисляем пару (xi+1=f(xi), x2(i+1)=f(f(x2i))). Как только получаем пару одинаковых значений xm=x2m, заключаем, что m\s, где s – период последовательности. Кроме того, если l – длина предпериода последовательности (то есть количество первых членов последовательности, пока та не вошла в цикл), то m=s 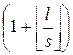 .
.
Этот метод позволяет сэкономить память для последовательностей большого периода. Действительно, одновременно следует хранить лишь два члена последовательности. Если бы поиск периода велся традиционным способом (последовательного вычисления всех членов последовательности до первого повторения), то потребовалось бы место для хранения l+s членов.
Алгоритм Ро-метода Полларда для факторизации.
Вход: n – составное число.
f(x)=x2+1 mod n.
Ш.1. x1=2, x2=2.
Ш.2. Вычислить x1=f(x1), x2=f(f(x2)).
Ш.3. Если x1=x2, то выбрать другой полином (например, f(x)=Ax2+C mod n (A, C - константы)) и снова начать алгоритм с Шага 1.
Ш.4. Вычислить d=НОД(x1—x2, n).
Ш.5. Если d=1, то вернуться на Шаг 2.
Выход: d\n.
Пример:
n=533.
| x1 | |||||
| x2 | |||||
| abs(x1—x2) | - | ||||
| d | - |
Нашли нетривиальный делитель числа n: d=13.
Ответ: 533=13·41.
Замечание: Если f(x) генерирует псевдослучайную последовательность (а это так, если f(x)=Ax2+C mod n и A, B, n – попарно простые числа, то f(x) – линейный конгруэнтный генератор), то сложность данного метода составляет О( 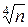 ) модулярных умножений.
) модулярных умножений.
Ро-метод Полларда может быть применен и для факторизации на конечном множеством многочленов.
2.5. p—1 – метод Полларда.
Данный метод является методом специального назначения для нахождения р - простого делителя составного числа n, для которого p—1 есть B-гладкое число.
Число a называется B-гладким, если все его простые делители не превышают B.
Идея метода заключается в следующем: зададим целое число B≤ 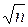 . Возьмем какое-нибудь простое число q≤B и возведем его в такую максимально возможную целочисленную степень, чтобы результат не превышал n. Очевидно, показатель этой степени будет
. Возьмем какое-нибудь простое число q≤B и возведем его в такую максимально возможную целочисленную степень, чтобы результат не превышал n. Очевидно, показатель этой степени будет 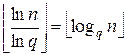 . Зададим число Q следующим образом:
. Зададим число Q следующим образом:
Q= 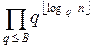 .
.
Если p – простой делитель числа n, для которого p—1 является B-гладким, то (p—1)\Q. Согласно теореме Ферма, для всех a: НОД(a,p)=1 выполняется aQ≡1(mod p). Поэтому если d=НОД(aQ—1,n)≠n, то d – нетривиальный делитель n. Если же d=n, то метод дает отказ.
Граница B выбирается исходя из вычислительных возможностей и априорных сведений о факторизуемом числе. На практике часто выбирают B между 105 и 106.
Алгоритм p—1 – метода Полларда:
Вход: n – нечетное составное число, не являющейся степенью целого числа.
Ш.1. Выбрать границу B. Составить таблицу простых чисел, меньших или равных B (если такой таблицы не имеется).
Ш.2. Выбрать случайное число a: 1<a<n. Вычислить d=НОД(a,n). Если d>1, то идти на Выход.
Ш.3. Для каждого простого q≤B вычислить l= 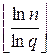 и a=a·ql mod n.
и a=a·ql mod n.
Ш.4. Вычислить d=НОД(a—1,n).
Ш.5. Если d=1 или d=n, то отказ.
Выход: d – нетривиальный делитель n.
Пример.
n=5945.
Ш.1. В=10. Простые числа, меньшие 10: 2, 3, 5, 7.
Ш.2. а=17. НОД(17,5945)=1.
Ш.3.
| q | ||||
| l | ||||
| ql mod n | ||||
| a |
a=2020.
Ш.4. d=НОД(2020, 5945)=5.
Ответ: 5945=5·1189.
Замечание: Сложность данного алгоритма составляет O 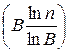 умножений по модулю.
умножений по модулю.
Дата добавления: 2015-11-28; просмотров: 3594;
