Определение расположения линии второго порядка по отношению к прямоугольной системе координат
Для определения расположения линии второго порядка, заданной общим уравнением 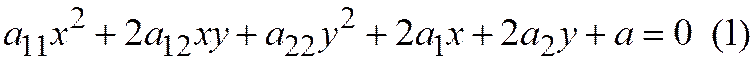
относительно ДПСК, достаточно знать параметры, характеризующие данную линию и ту систему координат, в которой уравнение линии является каноническим.
Если уравнение (1) является уравнением эллипса, то надо найти его полуоси, центр и направление оси, на котором лежат его фокусы.
Если уравнение (1) является уравнением гиперболы, то надо найти её полуоси, центр и направление действительной оси.
Если уравнение (1) является уравнением параболы, то надо найти её параметр, вершину и направление одного из двух лучей оси, например того, на котором лежит фокус.
Если линия сводится к одной точке, то надо найти её координаты.
Наконец, если линия распадается на две действительные прямые, то надо найти (в данной системе координат) уравнение каждой из них.
Если в уравнении (1)  , то расположение линии определяется при помощи параллельных переносов по осям
, то расположение линии определяется при помощи параллельных переносов по осям 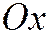 и
и 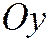 . Если в уравнении (1)
. Если в уравнении (1)  , то надо повернуть систему координат на угол
, то надо повернуть систему координат на угол 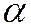 , чтобы в повёрнутой системе коэффициент
, чтобы в повёрнутой системе коэффициент 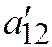 обнулился и затем опять при помощи параллельных переносов по осям
обнулился и затем опять при помощи параллельных переносов по осям 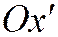 и
и 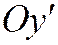 привести уравнение к одному из следующих простейших видов:
привести уравнение к одному из следующих простейших видов:
I. 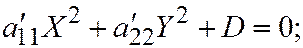 где
где 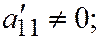
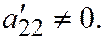
II. 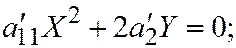 где
где 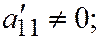
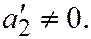
III. 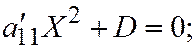 где
где 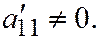
Ранее нами были найдены значения коэффициентов простейших уравнений (с помощью теории инвариантов) и их мы записали в следующем виде:
I. 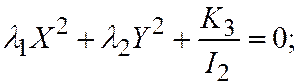
II. 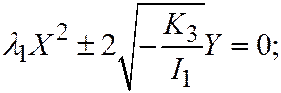
III. 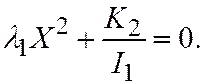
Угловой коэффициент новой оси 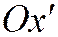 для каждого из простейших уравнений I, II, III линий второго порядка определяется по формуле:
для каждого из простейших уравнений I, II, III линий второго порядка определяется по формуле: 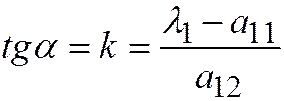 , (2)
, (2)
где 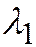 - тот корень характеристического уравнения, который является коэффициентом при
- тот корень характеристического уравнения, который является коэффициентом при 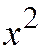 в простейших уравнениях.
в простейших уравнениях.
1. Эллипс. Если уравнение (1) является уравнением эллипса, то простейшее уравнение имеет вид:
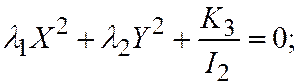 (
( 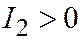 ,
,  ).
).
Считая, что через 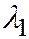 обозначен меньший по абсолютной величине корень характеристического урав-нения (
обозначен меньший по абсолютной величине корень характеристического урав-нения ( 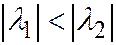 ), и переписывая последнее уравнение в виде:
), и переписывая последнее уравнение в виде: 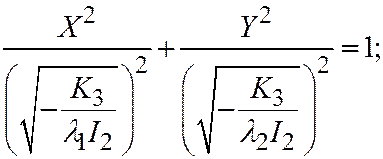 или
или 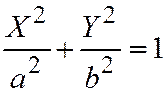 ,
,
где 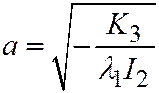 ,
, 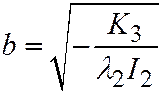 , заключаем, что
, заключаем, что 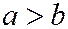 .
.
Так что по формуле (2) определяется угловой коэффициент большей оси эллипса.
Координаты центра эллипса находятся из системы:
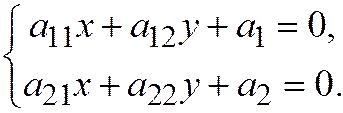 (3)
(3)
1. Гипербола. Если уравнение (1) является уравнением гиперболы, то простейшее уравнение имеет вид:
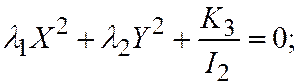 (
( 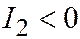 ,
,  ).
).
Обозначая через 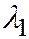 тот из корней характеристического уравнения, который имеет тот же знак, что и
тот из корней характеристического уравнения, который имеет тот же знак, что и 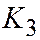 , перепишем последнее уравнение в виде:
, перепишем последнее уравнение в виде: 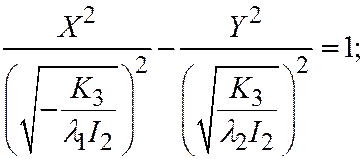 или
или 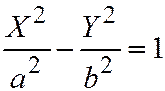 ,
,
где 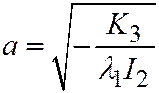 - действительная полуось,
- действительная полуось,  - мнимая полуось.
- мнимая полуось.
По формуле (2) определяется угловой коэффициент действительной оси гиперболы.
Координаты центра гиперболы находятся из системы: 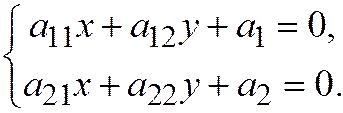 (3)
(3)
3. Парабола. Если уравнение (1) является уравнением параболы, то простейшее уравнение имеет вид:
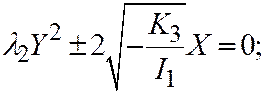 (
( 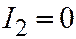 ,
,  ). Здесь
). Здесь 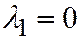 ,
,  .
.
По формуле  определяется угловой коэффициент оси параболы. Параметр параболы определяется по формуле
определяется угловой коэффициент оси параболы. Параметр параболы определяется по формуле 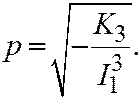
Координаты вершины параболы находятся так: возьмём на параболе точку 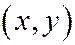 . Координаты вектора
. Координаты вектора 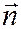 , нормального к касательной к параболе в этой точке таковы:
, нормального к касательной к параболе в этой точке таковы:  (т.к. уравнение касательной в точке
(т.к. уравнение касательной в точке 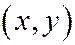 имеет вид:
имеет вид: 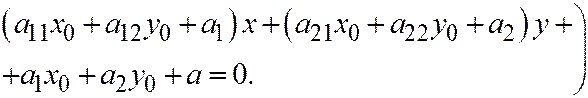 .
.
Для того чтобы точка 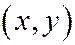 являлась вершиной параболы, необходимо и достаточно, чтобы вектор
являлась вершиной параболы, необходимо и достаточно, чтобы вектор 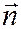 имел направление диаметров параболы (асимптотическое направление), т.е. чтобы выполнялось условие:
имел направление диаметров параболы (асимптотическое направление), т.е. чтобы выполнялось условие:
 (4). (Мы с вами ранее установили, что для параболы вектор
(4). (Мы с вами ранее установили, что для параболы вектор 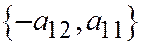 имеет направление, параллельное оси параболы). Теперь, умножая первое равенство в системе (4) на
имеет направление, параллельное оси параболы). Теперь, умножая первое равенство в системе (4) на 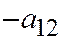 , второе – на
, второе – на 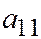 и складывая их почленно, будем иметь:
и складывая их почленно, будем иметь:
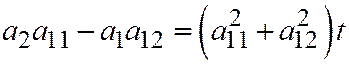 , откуда:
, откуда:
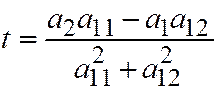 (5)
(5)
Переписывая уравнение параболы в виде:
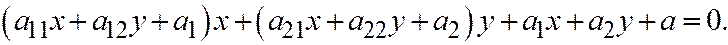
В силу соотношений (4) имеем:
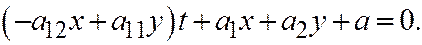 (6)
(6)
Таким образом, для нахождения координат вершины параболы надо решить линейную систему (4), (6), где 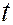 определяется по формуле (5). То есть. Сначала находим
определяется по формуле (5). То есть. Сначала находим 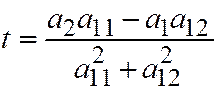 , подставляем его в систему:
, подставляем его в систему: 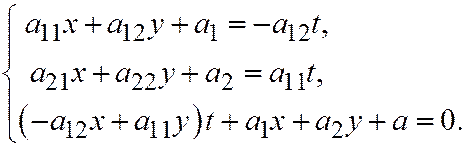 (7)
(7)
В этой системе одно уравнение обязательно окажется лишним, и координаты вершины параболы определятся однозначно.
И последнее. Вектор, направленный по оси параболы в сторону её вогнутости определяется из соотношения: 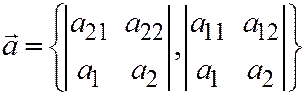 .
.
Дата добавления: 2016-01-20; просмотров: 1157;
