Распределение времени пребывания в проточных реакторах

Говоря о времени пребывания реагентов в реакторе, мы имеем в виду некоторую среднюю величину. Исключение составляет лишь модель РИВ, в которой все частицы пребывают в реакторе одинаковое время. Для РИС и реальных реакторов, описываемых диффузионными и ячеечной моделями, время пребывания отдельных частиц в реакторе может быть разным. Это время зависит от траектории, которую описывает каждая частица потока в своем движении от входа к выходу. Чем сложнее эта траектория, тем большим оказывается время пребывания. В свою очередь, траектория движения частицы зависит от гидродинамики потоков (неравномерности распределения скоростей и давлений, турбулентности, внутренних течений, вызванных градиентами концентраций, температур, поверхностного натяжения и др.). Таким образом, очевидно, что для РИС и реальных реакторов время пребывания является случайной величиной и может быть описано только с помощью вычислительного аппарата математической статистики.

Непрерывная случайная величина может быть задана с помощью функций распределения случайной величины. Различают интегральную функцию распределения F(τ) и дифференциальную функцию распределения или плотность распределения f(τ).

Интегральная функция распределения – это объемная доля потока, выходящего из реактора, которая находилась в нем в течении времени, меньшим, чем τ. Свойства этой функции:

при τ₂ > τ₁ F(τ₂) ≥ F(τ₁)

F(0) = 0 F(∞) = 1

Производная от этой функции 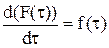называется плотностью распределения. Среднее время пребывания частицы в реакторе при использовании функций распределения можно рассматривать как математическое ожидание непрерывной случайной величины.

Экспериментально функции распределения времени пребывания могут быть найдены путем исследования так называемых кривых отклика. Суть этого метода состоит в следующем. На входе в реактор создается некоторое возмущение. Таким возмущением является введение в основной поток вещества (индикатора), отличающегося по какому-либо свойству: окраске, электропроводности, оптической плотности, кислотности, радиоактивности и т.д.). Индикатором может быть вещество, которое не изменяется и не поглощается в ходе эксперимента; концентрация его должна легко контролироваться.

Возмущение на входе (входной сигнал) может быть ступенчатым или импульсным.

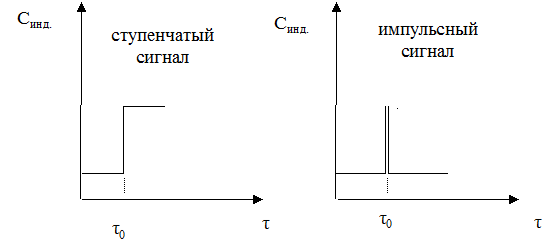
Для получения кривой отклика на входной сигнал (выходного сигнала) измеряют в разные моменты времени концентрацию индикатора в потоке, выходящим из реактора.

С_инд. = f(τ)

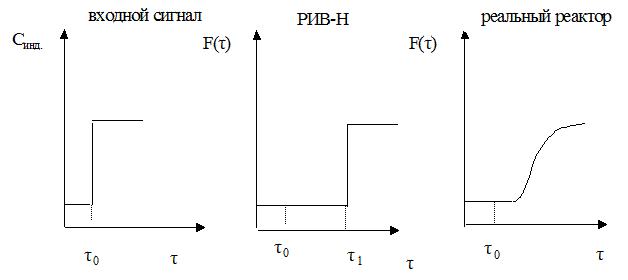
Выходной сигнал при ступенчатом входном сигнале используют для определения интегральной функции распределения F(τ); дифференциальная функция распределения f(τ) соответствует кривой отклика на сигнал импульсной формы.

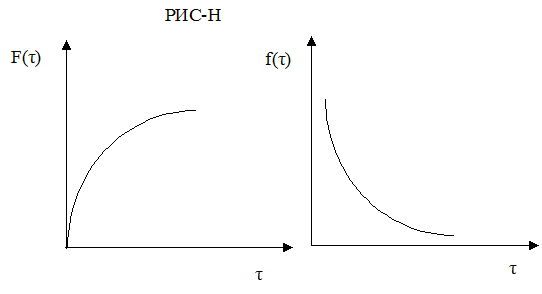
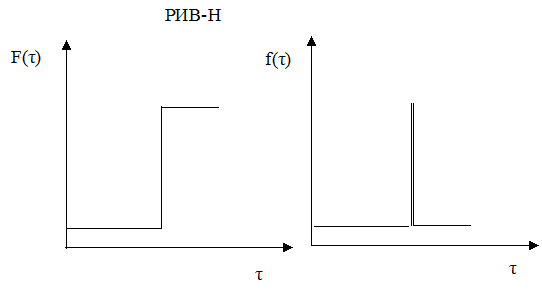
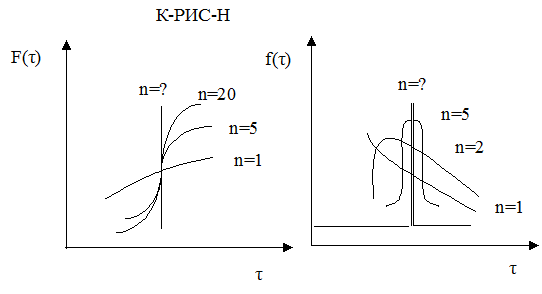
Сравним кривые отклика для идеального и реального реактора вытеснения.

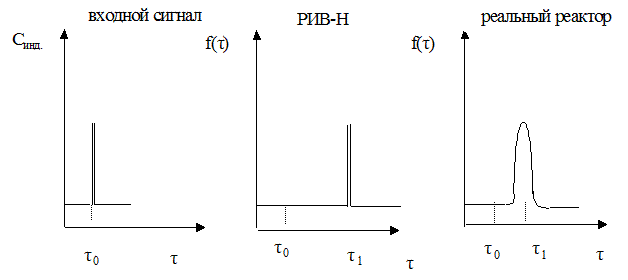
На основе функций распределения можно рассчитать среднее время пребывания частиц реагентов в проточном реакторе, определить тип модели. Учесть отклонение от этой модели и т.д.

Лекция № 14