БАЙЕСОВСКИЕ ПРОЦЕДУРЫ РЕШЕНИЯ

Предположим, что частичное описание выбранного случайным образом объекта есть 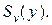Необходимо установить правило для определения класса, к которому следует отнести этот объект. Совместная вероятность того, что частичное описание 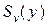удовлетворит последовательности длиной 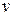, а объект относится к классу 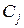, равна

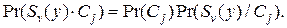
Поскольку нам задана последовательность наблюдений, а не вероятность определенных классов 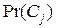приемлемой для нашего случая формулы

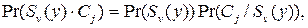
следует специальный случай байесовского правила

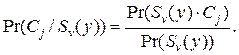(64)

Знаменатель правой части (64) есть сумма вероятностей наблюдения последовательности в каждом классе, взвешенных с вероятностью появления каждого класса:

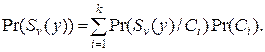(65)

Таким образом, получаем в окончательном виде формулу Бейеса для случая последовательной классификации образов

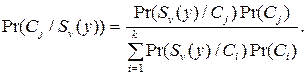(66)

Ожидаемые потери, связанные с решением отнести объект, удовлетворяющий последовательности 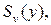к классу 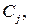равны

EL 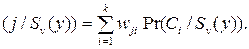(67)

Оптимальное байесовское правило классификации определяет класс 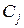, для которого выражение (67) минимальное.

Эти рассуждения применимы в случае, когда уже установлена последовательность наблюдений и выбраны оценки вероятностей, которые будут использованы, так что минимизация функции (67) есть правило классификации образов. Цель процедур распознавания образов – найти наилучшие последовательности и соответствующие правила классификации.