ПРИМЕР РЕШЕНИЯ ЗАДАЧИ ДЛЯ АЛГОРИТМА ОГРАНИЧЕННОГО ПРОСМОТРА ВПЕРЕД

Для реализации как оптимальной, так и приближенной процедуры классификации «просмотра вперед» необходимо определять условные и маргинальные вероятности. На практике их можно оценить по наблюдаемым частотам в выборке S. Проиллюстрируем сказанное примером, в котором в качестве выборки S берется множество четверок (табл. 9). Процедура классификации иллюстрируется данными табл. 10.

Таблица 9

Для простоты стоимость ошибочной классификации принимается равной 0, если классификация является верной, и равной 1 в противном случае. Предполагается, что стоимость измерения равна 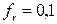при всех r. Для стоимости ошибочной классификации имеем

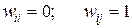для всех .

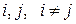Таблица 10

Данные перекрестной классификации («классы – частоты выборки» измерений)
для просмотра на один шаг вперед

Измерение 1: ожидаемые потери равны 0,435 + 0,1 = 0,5375 > 0,5
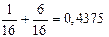
Буква	Класс 1	Класс 2
H
G
E
W
Итого
Измерение 2: ожидаемые потери равны 0,5 + 0,1 = 0,6 ( )
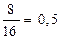Буква	Класс 1	Класс 2
X
K
L
S
Итого

Продолжение таблицы 10

Измерение 3: ожидаемые потери равны 0,3125 + 0,1 = 0,4125 < 0,5
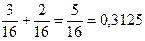
Буква	Класс 1	Класс 2
Q
B
F
T
Итого
Измерение 4: ожидаемые потери равны 0,25 + 0,1 = 0,35 < 0,5
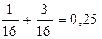
Буква	Класс 1	Класс 2
A
R
M
Z
Итого

Априорные сведения о принадлежности четверок букв различным классам приведены в табл. 9. В случае равных значений частот появления событий выбирается класс 1. Определение ожидаемых потерь, вызванных результатом только одного измерения и последующей классификации, необходимо для того, чтобы быть уверенным, что после выполнения этого измерения проводятся наилучшие возможные классификации. В рассматриваемом примере мы исходим из данных классификации и соответствующих тестов, представленных в табл. 10. Отнесение любой буквы к классу 1 или 2 осуществляется по большему относительному значению случаев нахождения данной буквы в соответствующем ряду по всему множеству четверок. Например, в измерении 1 принадлежность буквы H к первому классу может быть оценена вероятностью 2/16, соответственно, для такого решения получаем ожидаемые потери, равные 1/16. При равных случаях появления буквы для обоих классов выбирается класс 1. Правильность выбранной в нашем примере процедуры классификации подтверждается уменьшением оценки ожидаемых потерь в процессе измерений.