Прямое и обратное преобразование логического и арифметического выражений

При преобразовании логического выражения в арифметическое его значение считается равным 1 в случае, когда логическое значение есть истина, и равно 0 в противном случае. Например, если 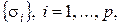– множество предикатов, а 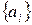– множество вещественных чисел, то сумма 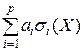– трансформируется в сумму только тех чисел, которым соответствуют предикаты 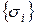со значениями истина.

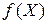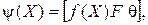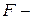В случае преобразования арифметического выражения в логическое предикат записывается следующим образом: где арифметическое соотношение, а 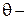величина постоянная.

Линейные предикаты имеют вид

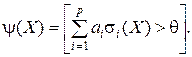(54)

Выражение (54) определяет предикат 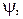линейный относительно множества 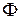частных предикатов. Обозначим множество всех таких предикатов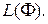

7.2. ПЕРСЕПТРОНЫ ОГРАНИЧЕННОГО ПОРЯДКА

Персептрон – это гипотетическое устройство, которое может вычислить все предикаты, линейные относительно фиксированного множества частных предикатов (определение № 2). Линейный предикат является правилом классификации, так как он относит любые изображения X либок классу 0, либо к классу 1.

Персептрон называется ограниченным k-го порядка, если носители его предикатов 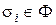состоят не более чем из k точек, т. е. этим значением ограничивается множество точек в сетчатке R, на которые «смотрит» каждый отдельный предикат при классификации изображения. Порядок устройства указывает на степень сложности его элементарных операций. Когда некоторый предикат 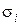персептрона «смотрит» на всюсетчатку, его порядок равен числу точек в R. Поскольку на сложность предиката 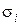, за исключением его порядка, нет ограничений, такой предикат мог бы просто быть отображением, показывающим для каждого из 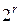возможных изображений X, должна ли соответствующая классификация быть 0 или 1. Если порядок персептрона меньше размера сетчатки, т. е. отсутствует соответствующий сильный предикат, то существование линейного предиката для каждой из 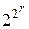возможных классификаций не гарантировано. Из этого вытекает необходимость определения круга задач, для которых возможно формирование линейных комбинаций логических функций локальных свойств изображения X, чтобы осуществлять классификацию, основанную на его глобальном смысле.

Предикат 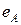называется маской, если он принимает значение истина, тогда и только тогда, когда все точки конечного множества 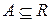являются единицами, т. е. находятся в «возбужденном» состоянии. Определим 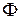как множество предикатов 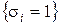для всех 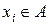. В связи с тем, что предикаты множества 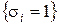могут иметь общие элементы (переменные), линейный предикат – маска 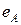определяется так:

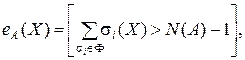
где N(A) – число элементов множества A.

Размером маски назовем число элементов ее носителя.

Поскольку распознавание образов состоит из выделения признаков и приписывания им весов, важно предположить возможный подход к распознаванию при фиксированных ограничениях на сложность указанных этапов. Ограничение линейными весовыми функциями и ограничение на порядок персептрона задают систему выбора весов и определяют сложность выделения признаков.

Изучение персептронов конечного порядка целесообразно по двум причинам. С одной стороны, соответствующие теоремы позволяют установить ограничения линейных машин, которые можно в принципе построить. С другой стороны, доказательство соответствующих теорем может служить иллюстрацией применимости используемых методов для анализа возможностей систем искусственного интеллекта.

7.2.1.Теорема о масках (теорема о
положительной нормальной форме)

Если 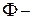какое-то множество масок, то каждый предикат 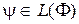линеен относительно всех масок, а его порядок определяется размером наибольшей маски из множества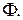

Доказательство. Любую булеву функцию 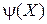на множестве 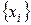логических переменных 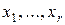из сетчатки 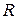можно записать в дизъюнктивной нормальной форме

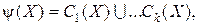
где каждое 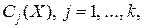поскольку – логические произведения 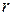членов. Все эти произведения различны, наша задача состоит в доказательстве того, что самое большое из логических произведений 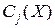будет истинным, т. е.

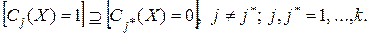
Следовательно, 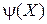можно записать в линейной форме

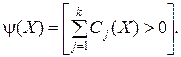
Все C_j можно представить в виде линейной комбинации масок, поэтому 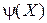будет линейной комбинацией линейных комбинаций и, следовательно, линейной на множестве масок. Покажем, что этим же свойством обладают все C_j. Любое логическое произведение C_j можно записать как произведение переменных и их отрицаний:

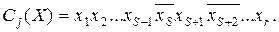(55)

Пусть 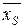– первое отрицание, тогда (55) можно представить в виде

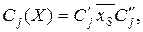(56)

где 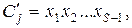(57)

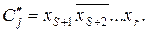(58)

Очевидно отличие 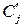и 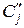: если 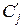содержит только сами переменные, то 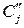включает как переменные, так и их отрицания. Алгебраические преобразования дают

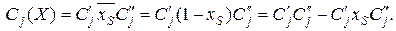(59)

В линейной комбинации двух логических произведений, содержащихся в выражении (59), только во втором из них присутствует переменная x_s, т. е. каждое преобразование типа (59) устраняет одно отрицание. Если проделать эту процедуру со всеми C_j и со всеми выведенными из них логическими произведениями, а затем со всеми последующими произведениями и т. д., то в итоге 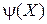будет линейной комбинацией логических произведений, содержащих только переменные (а не их отрицания). Такие логические произведения как раз и являются масками. Теорема доказана.