ФУНКЦИИ ПЕРСЕПТРОНОВ ПРИ РЕШЕНИИ ЗАДАЧ РАСПОЗНАВАНИЯ ОБРАЗОВ

Вход для персептрона определяется как упорядоченное множество двоичных элементов, совокупность которых называют сетчаткой 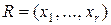. В отдельных случаях сетчатку R удобно представлять в виде матрицы с элементами x_ij – переменная в i-ой строке и j-м столбце. Такое представление обычно используется, когда двухмерная зависимость элементов существенна или когда данная интерпретация удобна для иллюстрации.

В отличие от большинства систем технического зрения, для которых элементы сетчатки x_i – это двоичный код интенсивности соответствующей точки изображения, в изображении X персептрона, представляющем собой совокупность значений элементов множества R, x_i принимает значения: 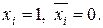Например, некоторое изображение X можно записать в виде 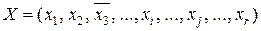. Если сетчатка имеет r переменных, то существует 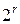возможных изображений. Каждое из этих изображений относится точно к одному классу из общего количестваклассов 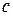. Число возможных комбинаций растет довольно быстро, так как отнести изображения к классам можно 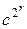способами.

Предикаты

Логическую функцию 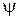, позволяющую преобразовывать изображения в бинарное множество {истина, ложь}, принято называть предикатом. Предикат может быть логической функцией от 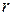двоичных переменных, при этом для вычисления значения 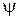часто используются не все, а лишь некоторые точки (переменные) из сетчатки 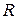. В таких случаях 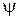называется частным предикатом, а множество переменных из сетчатки R, используемое для определения 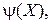называется носителем этого предиката.

Проиллюстрируем эти понятия на примере сетчатки, элементы которой расположены в виде квадрата (рис. 15). Допустим, интерес представляет предикат 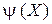, который содержит элементы на диагоналях матрицы (выделены жирным шрифтом). Очевидно, что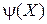
принимает значение истина тогда и только тогда, когда упомянутые элементы равны 1.

Локальный предикат 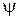характеризуется малым числом точек в носителе . Предикат 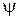называется конъюнктивно локальным, если существует такое множество 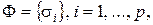локальных предикатов, что 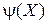можно представить в виде их конъюнкции (логической операцией И). Исследование конъюнктивно локальных предикатов осуществляется всякий раз, когда необходимо анализировать изображения сложной структуры, состоящей из различных фрагментов.

Порядок 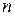предиката 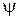определяется числом переменных 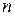носителя этого предиката.

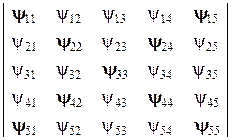
Рис. 15. Сетчатка, состоящая из 25 элементов,
представлена в виде квадрата 5´5