Матрица ролей в шкале порядка
| x | 11(4,5) | 6(2) | 9(3) | 11(4,5) | 4(1) | 109(6) |
| 11(4,5) | = | > | > | = | > | < |
| 6(2) | < | = | < | < | > | < |
| 9(3) | < | > | = | < | > | < |
| 11(4,5) | = | > | > | = | > | < |
| 4(1) | < | < | < | < | = | < |
| 109(6) | > | > | > | > | > | = |
В шкале наименований в качестве меры расстояния между объектами i и l, как и в предыдущем случае, используется разница ролей, которую они играют среди объектов множества A. При этом мера расстояний равняется
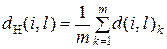 , (3)
, (3)
гдеd (i, l)k = 0, если (xik = «=» и xlk = «=»), или (xik = «≠» и xlk = «≠»),
d (i, l)k = 1, если (xik = «=» и xlk = «≠»), или (xik = «≠» и xlk = «=»).
Если в шкале наименований имеются следующие значения: x = a, b, a, a, c, b, – то 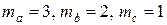 ; а расстояния между объектами равны:
; а расстояния между объектами равны:
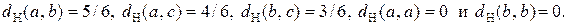
Для шкал разных типов в многомерном случае расстояние 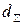 определяется, используя правило для евклидова расстояния:
определяется, используя правило для евклидова расстояния:
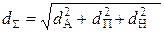 . (4)
. (4)
В ряде задач анализа данных, таких как корреляционный и регрессионный анализ, при обработке групповых экспертных оценок и других, необходимо оценивать расстояния между признаками. Далее рассматривается мера, пригодная для пар как однотипных, так и разнотипных признаков. Если признаки x1 и x2измерены в шкалах, более сильных, чем шкала порядка, то для определения расстояния между признаками используют то же самое выражение, что и для абсолютной шкалы:  , где r – модуль линейной корреляции между признаками x1 и x2, равный
, где r – модуль линейной корреляции между признаками x1 и x2, равный
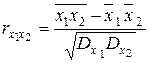 , (5)
, (5)
где 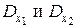 – дисперсии признаков x1 и x2 соответственно.
– дисперсии признаков x1 и x2 соответственно.
Для определения меры расстояния между двумя признаками, измеренными в шкале порядка, в наиболее распространенном варианте перебираются все сочетания 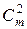 из m объектов по два и для каждой пары
из m объектов по два и для каждой пары
 сравнивают порядковое отношение между ними по признакам x1 и x2. Мера расстояния
сравнивают порядковое отношение между ними по признакам x1 и x2. Мера расстояния  между признаками устанавливается следующим образом:
между признаками устанавливается следующим образом:
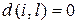 , если порядковые отношения одинаковы, когда (
, если порядковые отношения одинаковы, когда ( 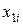 >
> 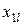 и
и 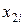 >
>  ), или (
), или ( 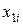 <
< 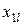 и
и 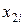 <
<  ), или (
), или ( 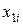 =
= 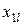 и
и 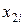 =
=  );
);
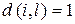 , если порядковые отношения на этих признаках прямо противоположны, т. е. (
, если порядковые отношения на этих признаках прямо противоположны, т. е. ( 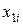 >
> 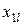 и
и 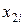 <
<  ), или (
), или ( 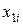 <
< 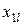 и
и 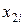 >
>  );
);
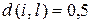 в промежуточном случае, когда по одному признаку имеет место отношение > или <, а по другому − отношение =.
в промежуточном случае, когда по одному признаку имеет место отношение > или <, а по другому − отношение =.
Общее расстояние определяется как средняя мера «несогласия» порядков по двум признакам на всех парах объектов:
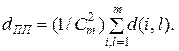 (6)
(6)
Общая мера расстояний между двумя разнотипными признаками определяется как средняя величина двух частных расстояний. Оба признака можно сделать однотипными, если один из них «обеднить» до более слабого, или второй «усилить» («оцифровать») до более сильного. Согласование разнотипных измерительных шкал по информативности рассмотрим на трех примерах.
Пример 1.Согласование признаков абсолютной шкалы и шкалы порядка
Когда из двух признаков один измеряется в «сильной» шкале 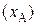 , а другой – в шкале порядка
, а другой – в шкале порядка 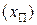 , ослабление дошкалы порядка
, ослабление дошкалы порядка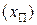 – преобразование «сильной» шкалы
– преобразование «сильной» шкалы 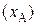 в шкалу
в шкалу 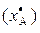 ,состоит в том, что числовые значения в шкале
,состоит в том, что числовые значения в шкале 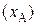 корректируются с учетом только отношения порядков. Усиление («оцифровка») шкалы порядка
корректируются с учетом только отношения порядков. Усиление («оцифровка») шкалы порядка 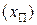 до сильной шкалы
до сильной шкалы 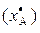 делается таким образом, чтобы: 1) порядок объектов по усиленному признаку
делается таким образом, чтобы: 1) порядок объектов по усиленному признаку 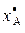 не противоречил порядку по исходному признаку
не противоречил порядку по исходному признаку 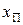 ; 2) числовыезначения признака
; 2) числовыезначения признака 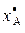 должны быть максимально коррелированными со значениями признака
должны быть максимально коррелированными со значениями признака 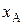 . Соответствующие преобразования числовых значений иллюстрируются табл. 3.
. Соответствующие преобразования числовых значений иллюстрируются табл. 3.
Таблица 3
Исходные значения и преобразованные
сочетания признаков в шкалах xAи xП
| № | xA | xП | 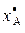
|
| 2,5 | 3,6 | ||
| 4,2 | 2,5 | 3,6 | |
| 5,1 | |||
| 5,1 | |||
| 0,4 | 5,1 | ||
| 5,1 | |||
В процессе преобразования значения шкалы 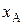 корректируются с учётом значений признаков в шкале
корректируются с учётом значений признаков в шкале 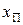 иразмещаются в шкале
иразмещаются в шкале 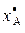 по возрастанию. Если в последовательности k объектов с порядковыми номерами от t до
по возрастанию. Если в последовательности k объектов с порядковыми номерами от t до 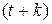 значения признаков в шкале
значения признаков в шкале 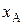 меньше, чем у объекта с номером
меньше, чем у объекта с номером 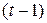 , то всем объектам в шкале
, то всем объектам в шкале 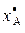 с порядковыми номерами от (t – 1) до (t + k) приписывается среднеарифметическое значение признака
с порядковыми номерами от (t – 1) до (t + k) приписывается среднеарифметическое значение признака 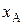 :
:
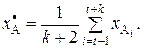 (7)
(7)
Если инверсий значений признаков 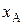 не было или они были устранены, осуществляется проверка наличия серий, т. е. последовательности из k объектов c одинаковым значением признака в шкале
не было или они были устранены, осуществляется проверка наличия серий, т. е. последовательности из k объектов c одинаковым значением признака в шкале 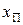 . При этом соответствующим значениям в шкале
. При этом соответствующим значениям в шкале 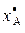 приписываются среднеарифметические значения их признака в шкале
приписываются среднеарифметические значения их признака в шкале 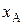 :
:
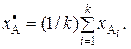 (8)
(8)
Одна инверсия в табл. 3 выделена в столбце 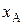 (строка 5 и 6), и две серии – в столбце
(строка 5 и 6), и две серии – в столбце 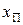 (строки 2 и 3, строки 9, 10 и 11).
(строки 2 и 3, строки 9, 10 и 11).
На основании данных, приведенных в табл. 3, определим расстояния между признаками: 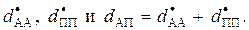 Расстояние
Расстояние 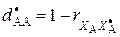 , где коэффициент линейной корреляции
, где коэффициент линейной корреляции
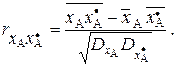 (9)
(9)
В результате вычислений получаем следующие значения:

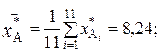
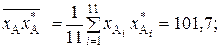
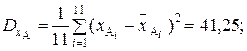
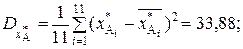
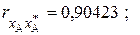
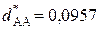 .
.
Аналогичным образом определяются значения:

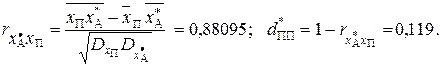
Таким образом, средняя мера расстояния между признаками  и
и 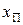 равна:
равна: 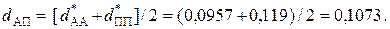
Пример 2. Согласование признаков абсолютной шкалы  и шкалы наименований
и шкалы наименований 
Преобразования исходных данных, необходимые для согласования признаков шкал  и
и 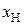 , приведены в табл. 4.
, приведены в табл. 4.
Таблица 4
Исходные значения и преобразованные сочетания
признаков объектов в шкалах xAи xH
| Исходные значения | Ослабление | Усиление | |||
| xA | xH | x*H | xH | xA | x*A |
| 3,5 | c | p | c | 3,5 | 3,5 |
| 2,6 | b | p | b | 2,6 | 4,6 |
| a | k | a | 1,3 | ||
| 8,3 | b | s | b | 8,3 | 4,6 |
| 2,8 | b | p | b | 2,8 | 4,6 |
| 1,6 | a | k | a | 1,6 | 1,3 |
При преобразовании признаков 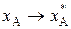 , если
, если  соответствует единственному признаку
соответствует единственному признаку 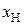 (например, с), то
(например, с), то 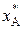 =
= 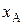 . Если одинаковое имя (например, b) встречается несколько (t) раз, всем соответствующим признакам устанавливается величина
. Если одинаковое имя (например, b) встречается несколько (t) раз, всем соответствующим признакам устанавливается величина
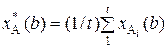 . (10)
. (10)
Следовательно, имеют место следующие значения: 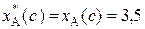 ,
,
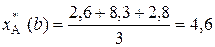 ,
, 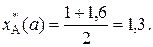
По представленным в табл. 4 числовым значениям признаков  и
и 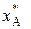 вычисляем следующие величины:
вычисляем следующие величины:
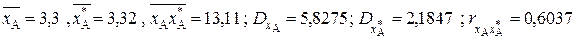 .
.
В итоге расстояние между признаками 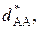 вычисленное через коэффициент линейной корреляции, равно
вычисленное через коэффициент линейной корреляции, равно
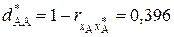 .(11)
.(11)
При формировании ослабленного признака 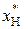 количество имен в нем должно быть таким же, как в исходном признаке
количество имен в нем должно быть таким же, как в исходном признаке 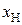 . Это обеспечивается решением задачи кластеризации значений признаков
. Это обеспечивается решением задачи кластеризации значений признаков 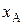 на t кластеров. Далее для вычисления расстояния
на t кластеров. Далее для вычисления расстояния 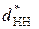 сформируем матрицы смежностей, одну из которых построим по признаку
сформируем матрицы смежностей, одну из которых построим по признаку 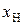 , а вторую – по признаку
, а вторую – по признаку 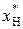 (табл. 5).
(табл. 5).
Таблица 5– Матрица ролей в шкалах наименований 
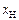
| c | b | a | b | b | a |
| c | = | ≠ | ≠ | ≠ | ≠ | ≠ |
| b | ≠ | = | ≠ | = | = | ≠ |
| a | ≠ | ≠ | = | ≠ | ≠ | = |
| b | ≠ | = | ≠ | = | = | ≠ |
| b | ≠ | = | ≠ | = | = | ≠ |
| a | ≠ | ≠ | = | ≠ | ≠ | = |
Величина 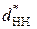 вычисляется по формуле
вычисляется по формуле
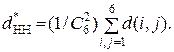 (12)
(12)
В матрице ролей, приведенной в таблице 5, выделены ячейки (отличающиеся по наименованиям), соответствующие 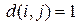 . Так как
. Так как 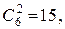 а
а 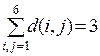 , в итоге получаем
, в итоге получаем 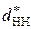 = 0,2. Средняя мера расстояния между признаками равна
= 0,2. Средняя мера расстояния между признаками равна
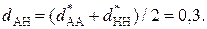
| (13) |
Пример 3. Согласование признаков объектов в шкалах порядка и наименований
В рассматриваемом примере информация предъявляется в шкале порядка 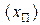 и в шкале наименований
и в шкале наименований 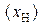 (табл. 6); ослабление шкалы
(табл. 6); ослабление шкалы 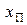 до шкалы
до шкалы 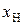 осуществляется по схеме предыдущего случая разделением порядковых позиций на 3 кластера, количество которых равняется числу различных имен в признаке
осуществляется по схеме предыдущего случая разделением порядковых позиций на 3 кластера, количество которых равняется числу различных имен в признаке 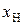 (a, b и d).
(a, b и d).
Таблица 6
Исходные и преобразованные признаки объектов в
шкалах порядка и наименований
| Исходные значения | Ослабление признаков | Усиление признаков | ||||
| хП | хН | 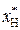
| 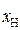
| № | 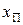
| 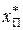
|
| a | c | a | ||||
| b | a | b | 2,5 | |||
| d | a | d | 4,5 | |||
| b | a | b | 2,5 | |||
| d | d | d | 4,5 |
Первоначально признак канонизируется до нормированных рангов: для одиночного объекта (первая строка) 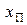 = 1, для серии из 3 одинаковых объектов (вторая, третья и четвертая строки)
= 1, для серии из 3 одинаковых объектов (вторая, третья и четвертая строки) 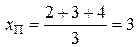 , для объекта (пятая строка)
, для объекта (пятая строка) 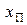 = 5, т. е. порядковому номеру. При усилении признака
= 5, т. е. порядковому номеру. При усилении признака 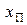 до признака
до признака 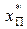 для одиночного объекта
для одиночного объекта
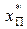 (а) =
(а) = 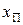 (a) = 1;
(a) = 1; 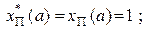 для серии из t одинаково поименованных объектов
для серии из t одинаково поименованных объектов 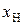 имеем
имеем 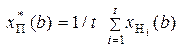 , причем вместо имен
, причем вместо имен 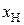 объектам ставятся в соответствие их порядковые номера.
объектам ставятся в соответствие их порядковые номера.
По представленным в таблице 5 значениям признаков 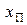 и
и 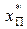 вычисляем следующие величины:
вычисляем следующие величины:
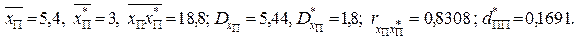
На основании рассмотрения матриц ролей в шкале наименований определяем расстояние 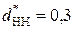 и среднее расстояние между признаками
и среднее расстояние между признаками
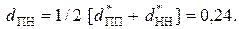 (14)
(14)
Таким образом, применение рассмотренных мер расстояния между объектами и между признаками позволяет использовать математическое обеспечение, разработанное для анализа таблиц данных с признаками, обозначенными в сильных шкалах.
Дата добавления: 2016-01-20; просмотров: 946;
