СРАВНЕНИЕ И СОГЛАСОВАНИЕ ПО ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ ШКАЛ РАЗЛИЧНОГО ТИПА

Для сравнения информативности шкал различного типа обычно определяют количество возможных неизоморфных протоколов, которые можно получить на языке этих шкал при заданных значениях m и n, где
m – число возможных состояний прибора, который измеряет некоторое свойство у n объектов. Например, протоколы <3,12> и <4,16> в абсолютной шкале будут неизоморфными, а в шкалах отношений, порядка и наименований – одинаковыми (изоморфными). Если 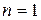, то независимо от типа шкалы количество неизоморфных протоколов равно m.

По данной методике проведено сравнение количества неизоморфных протоколов s_П, s_Н и s_А для шкал трех типов, соответственно: порядковой, наименований и абсолютной. Установлено, что при фиксированном числе градаций m с ростом количества исследуемых объектов n отличие по информативности различных шкал уменьшается. Отношение s_Н/s_Апри этом изменяется незначительно и остается малым, тогда как отношение s_П/s_А растет быстро и при n > 5 m достигает величины 0,9. Таким образом, в экспериментах с большим числом объектов информативность шкалы порядка приближается к информативности абсолютной шкалы.

В связи с тем, что в реальных задачах шкалы отношений и интервалов используются достаточно редко, далее материал излагается только применительно к трем из описанных типов шкал: абсолютной, порядковой и наименований.

Рассмотрим характерный для реальных задач случай, когда свойства изучаемых объектов измеряются с использованием различных, в том числе порядковых и номинальных шкал. Остановимся на непростой проблеме оценки меры расстояния как между объектами (строками информационной матрицы), так и между свойствами (столбцами этой матрицы) при обработке разнотипных шкал. Прежде рассмотрим представление данных без искажения их содержания в шкалах порядка и наименований.

В шкале порядка при всех допустимых преобразованиях для этой шкалы f_Потношения из набора < , >, = между двумя числами x_i и x_l должны сохраняться и для чисел f_П(x_i) и f_П(x_l). В матрице размером m × m
(m – число объектов в выборке А) в i-й строке указывается, в каких порядковых отношениях находится i-й объект ко всем остальным объектам выборки А или какую порядковую роль играет он в соответствующей матрице ролей. Два объекта считаются одинаковыми, если они имеют одинаковые порядковые отношения со всеми другими объектами. При анализе содержания элементов на пересечении k-го столбца с i-й и l-й строками суммарное и усредненное различие в отношениях i-го и l-го объектов оценивается в соответствии с выражениями:

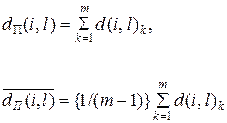, (2)

где d (i, l)_k = 0, если (x_ik = “<” и x _{l k} = “<”), или (x_ik = “>” и x_lk = “>”), или (x_ik = “=” и x_lk = “=”);

d(i, l)_k = 1, если (x_ik = “<” и x_lk = “>”), или (x_ik = “>” и x_lk = “<”);

d(i, l)_k = 0,5, если (x_ik = “=” и x_lk = “<,>”), или (x_ik = “<,>” и x_lk = “=”).

Данные, имеющие в шкале порядка следующие значения: x = 11, 6, 9, 11, 4, 109 – приведены в табл. 2. Те же данные в нормированных рангах (в скобках) соответственно равны: x' = 4,5, 2, 3, 4,5, 1, 6. В обеих шкалах расстояние между 2-й и 3-й строкой равно 1, а между 5-й и 6-й – 5.

Таблица 2