ПРИМЕНЕНИЕ ПОИСКА С ВОЗВРАТОМ ПРИ РЕШЕНИИ ЗАДАЧ УО
Задача называется коммутативной, если порядок применения любого конкретного множества действий в процессе ее решения не влияет на результат. Поскольку задачи УО обладают свойством коммутативности, во всех алгоритмах поиска их решений преемники формируются с учетом возможных присвоений только для единственной переменной в каждом узле дерева поиска.Например, в задаче раскрашивания карты Австралии в корневом узле дерева поиска можно осуществлять выбор между значениями SA = red, SA = green и SA = blue. Нельзя выбирать между значениями SA = red, и WA = blue, так как при этом вынужденные значения получают переменная NT = green и переменная Q = blue, а для переменной NSW не оставляется допустимых значений. При выполнении данного условия можно рассчитывать сократить количество листьев дерева решений до значения dn.
Поиск (в глубину) с возвратами имеет место, когда каждый раз выбираются значения для одной переменной и выполняется возврат, если больше не остается допустимых значений для присвоения другой переменной.В соответствующем алгоритме по существу используется метод инкрементного формирования преемников по одному преемнику за один раз, т. е. при формировании преемника текущее присвоение дополняется, а не копируется. Часть дерева поиска для задачи раскраски карты Австралии показана на рис. 35, где значения присваиваются переменным в порядке WA, NT, Q, ….
Такой недостаток простого неинформационного алгоритма поиска с возвратом, как низкая производительность, устраняется при использовании в них эвристических функций, соответствующих предметной области. Однако задачи УО можно решать эффективно и без знаний о конкретной проблемной области. Разработанные с этой целью методы общего назначения позволяют найти ответы на перечень следующих вопросов:
· Какой переменной должно быть присвоено значение в следующую очередь и в каком порядке необходимо пытаться присваивать эти значения?
· Влияют ли текущие присвоения значений переменным на другие переменные, которым значения еще не присвоены?
· Если достигнуто состояние, в котором ни одна переменная не имеет допустимых значений, т. е. какой-то путь оказался неудачным, позволяет ли поиск избежать повторения этой неудачи при прохождении последующих путей?
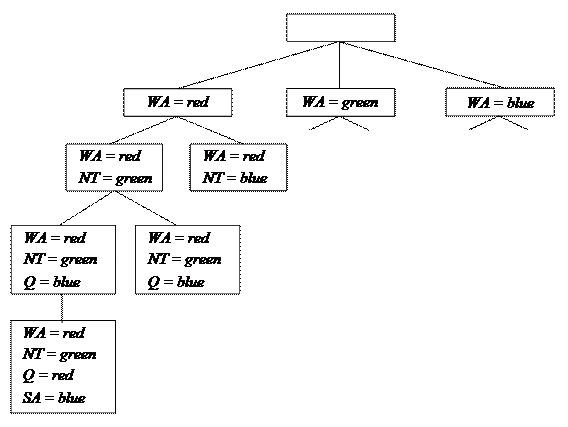
Рис. 35. Часть дерева поиска, сформированного путем простого поиска
с возвратами при решении задачи раскрашивания карты Австралии
Далее последовательно ответим на каждый из этих вопросов.
Содержащаяся в алгоритме поиска функция «выбор нераспределенных переменных» выбирает следующую переменную, которой еще не присвоено значение, в порядке, указанном в списке Variables. Такое статическое упорядочение переменных редко приводит к эффективному поиску. В частности, после присваивания WA = red и NT = green, остается только одно возможное значение для переменной SA, поэтому на следующем этапе целесообразно присваивать значение переменной Q = blue и выполнить присвоение SA = blue. Далее все варианты выбора значений переменных NSW и V становятся вынужденными.
Методика, согласно которой в первую очередь следует выбирать переменную, на которую распространяется наибольшее количество ограничений, называется эвристикой с минимальным количеством оставшихся значений(эвристикаМОЗ). Поиск с возвратом на основеМОЗповышает производительность от 3 до 3000 раз по сравнению с простым поиском с возвратом, в зависимости от задачи. При оценке производительности необходимо, однако, учитывать временные затраты на вычисление эвристической функции.
При выборе первого региона в задаче окрашивания карты Австралии эвристическая функция МОЗ не оказывает никакой помощи, поскольку первоначально каждый регион имеет три допустимых цвета. Для этого случая эвристика МОЗ предполагает выбор переменной, участвующей в наибольшем количестве ограничений (имеет большую степень) по сравнению с другими переменными. На рис. 34 переменной с наибольшей степенью 5 является переменная SA; другие переменные имеют степень 2 или 3, за исключением переменной T, которая имеет степень 0. В самом деле, после выбора переменной SA, задача решается без каких-либо неудачных этапов – теперь можно выбрать любой согласованный цвет в каждой точке выбора и все равно прийти к решению без поиска с возвратами.
В этом алгоритме, после выбора одной из переменных, необходимо принять решение о том, в каком порядке должны устанавливаться ее значения. Эффективность эвристики МОЗ обусловлена тем, что из рассмотрения исключается наименьшее количество вариантов выбора значений для соседних переменных в графе ограничений, т. е. предпринимается попытка сохранить максимальную гибкость для последующих присваиваний значений переменным.
До сих пор в рассматриваемом алгоритме поиска учет ограничений, распространяющихся на какую-либо переменную, осуществлялся только в тот момент, когда происходил выбор этой переменной. Если же рассматривать некоторые ограничения на предыдущих этапах поиска или даже до начала поиска, можно резко уменьшить пространство поиска. При каждом присваивании значения переменной X можно в процессе предварительной проверки просматривать каждую переменную Y, которая соединена с X и не имеет еще какого-либо значения. Из области определения переменной Y удаляется любое значение, которое является несовместимым со значением, выбранным для переменной X. Таким образом, предварительная проверка может рассматриваться как эффективный способ инкрементного вычисления той информации, которая требуется эвристике МОЗ для выполнения своей работы.
На рис. 36 показан поиск решения задачи раскрашивания карты с помощью предварительной проверки. После присваивания WA = red и
Q = green области определения переменных NT и SA сокращаются до единственного значения. После присваивания Q = green значение green удаляется из областей определения NT, SA и NSW. После присваивания
V = blue из областей определения NSW и SA удаляется значение blue, в результате чего переменная SA остается без допустимых значений, т. е.
область определения SA становится пустой. Поэтому предварительная проверка позволила обнаружить, что частичное присвоение
{WA = red, Q = green, V = blue} является несовместимым с ограничениями этой задачи, значит, алгоритм немедленно выполняет возврат.
| Начальные области определения | WA | NT | Q | NSW | V | SA | T |
| RGB | RGB | RGB | RGB | RGB | RGB | RGB | |
| После присваивания WA = red | R | GB | RGB | RGB | RGB | GB | RGB |
| После присваивания Q = green | R | B | G | R B | RGB | B | RGB |
| После присваивания V = blue | R | B | G | R | B | RGB |
Рис. 36. Поиск решения задачи с раскрашиванием карты на основе
предварительной проверки. Вначале выполняется присваивание WA = red,
затем предварительная проверка приводит к удалению значений red из
областей определения соседних переменных NT и SA
Дата добавления: 2016-01-20; просмотров: 641;
