ЗАДАЧИ УДОВЛЕТВОРЕНИЯ ОГРАНИЧЕНИЙ

Глава 15. ЗАДАЧИ УДОВЛЕТВОРЕНИЯ ОГРАНИЧЕНИЙ. ПОИСК С ВОЗВРАТОМ

В предыдущих главах рассматривались способы решения задач путем поиска в пространстве состояний, которые оцениваются с помощью эвристических функций, соответствующих данной проблемной области, и проверяется, не являются ли они целевыми состояниями. В этих алгоритмах поиска каждое состояние представляет собой черный ящик с неразличимой внутренней структурой данных, доступ к которой может осуществляться только с применением процедур, относящихся к соответствующей проблемной области: функции определения преемника, эвристической функции и процедуры проверки цели.

В задачах удовлетворения ограничений состояния соответствуют стандартному и очень простому представлению проверки цели, которое раскрывает структуры самой задачи и способствует более глубокому пониманию ее влияния на сложность решения. Это позволяет применять методы декомпозиции задачи и разрабатывать алгоритмы поиска, способные использовать для решения крупных задач эвристические функции общего назначения, а не функции, относящиеся к конкретной задаче.

Покажем, что рассмотрение состояний на более высоком уровне детализации, чем просто в виде «черных ящиков», приводит к обоснованию целого ряда новых методов решения задач [3].

ЗАДАЧИ УДОВЛЕТВОРЕНИЯ ОГРАНИЧЕНИЙ

С формальной точки зрения любая задача удовлетворения ограничений (УО) определена множеством переменных X₁, X₂, …, X_n, где любая переменная X_i имеет непустую область определения D_i возможных значений, и множеством ограничений C₁, C₂, …, C_m. Каждое ограничение C_i,помимонекоторого подмножества переменных, задает допустимые комбинации значений для этого подмножества. Еслиприсваивание значений некоторым или всем переменным (X_i = v_i, X_j, = v_j, …)не нарушает никаких ограничений, оно называется совместимым или допустимым присваиванием. Решением задачи УО является полное присваивание значений всем переменным и удовлетворение всех ограничений. Кроме того, для некоторых задач УО требуется найти решение, которое максимизирует целевую функцию.

Предположим, мы рассматриваем карту Австралии, на которой показаны все ее штаты и территории (рис. 34), и что необходимо раскрасить каждый регион в красный, зеленый или синий цвет таким способом, чтобы ни одна пара соседних регионов не имела одинаковый цвет из списка Variables: red, green, blue.

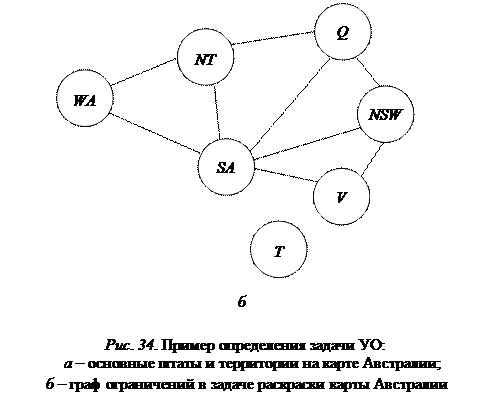
Сформулируем это задание в виде задачи УО. Переменными обозначим сокращенные названия регионов: WA, NT, Q, NSW, V, SA и T.Тогдаобластью определения каждой переменной будет являться множество цветов: red, green, blue, а ограничения состоят в том, что все пары соседних регионов не должны иметь одинаковый цвет. Например, допустимыми комбинациями для соседних регионов WA и NTявляются следующие пары:

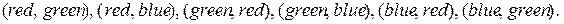
Из достаточно большого количества возможных решений этой задачи УО в качестве примера приведем следующее:

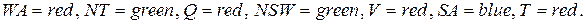
Рассматриваемая задача УО представлена визуально в виде графа ограничений (рис. 34, б), узлы которого соответствуют переменным, а дуги – ограничениям.

Поскольку состояния в задачах УО выражаются в виде множества переменных с присвоенными значениями (соответствует некоторому стандартному шаблону), можно разработать эффективные эвристические функции и записать в универсальной форме функцию определения преемника и процедуру проверки цели, применимой к задачам УО из различных проблемных областей. При использовании простейшего представления задачи УО в виде структуры графа ограничений можно в некоторых случаях добиваться экспоненциального уменьшения сложности решения задачи.

Любую задачу УО как стандартную задачу поиска можно сформулировать следующим образом:

· Начальное состояние. Пустое присваивание { }, в котором ни одной переменной не присвоено значение.

· Функция определения преемника. Любой переменной может быть присвоено значение, если она еще не присвоено, при условии, что переменная не будет конфликтовать с другими, ранее присвоенными значениями переменных.

· Проверка цели. Текущее присваивание является полным, поскольку участвует каждая переменная, которая удовлетворяет всем ограничениям.

· Стоимость пути. Постоянная стоимость (например, 1) для каждого этапа.

Поскольку каждое решение представляет собой полное присваивание, при наличии 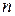переменных (преемников) оно находится на глубине n и, соответственно, дерево поиска распространяется только на глубину n. Для решения задач УО широко применяется алгоритм поиска в глубину, при этом сам путь, по которому достигается некоторое решение, может быть различным. Если максимальный размер области определения любой переменной в задаче УО равен d, то количество возможных полных присваиваний измеряется величиной O(dⁿ), т. е. зависит экспоненциально от количества переменных n.

В задачах УО простейшего вида используются переменные, которые являются дискретными и имеют конечные области определения. К такому классу относится задача раскраски географической карты. Рассмотренную ранее задачу с восемью ферзями можно также рассматривать как задачу УО с конечной областью определения, в которой переменные представляют собой позиции каждого ферзя на столбцах 1, …, 8, а каждая переменная имеет область определения {1, 2, 3, 4, 5, 6, 7, 8}.

Задачами УО с конечной областью определения являются также булевы задачи, в которых переменные могут иметь значения либо true,
либо false. Отдельной разновидностью булевых задач УО считаются некоторые NP-задачи (класс недетерминированных полиномиальных задач), а также задачи, для которых существует алгоритм, позволяющий выдвинуть гипотезу о возможном решении, затем проверяется правильность этой гипотезы с помощью полиномиальных затрат времени. Обычно нельзя рассчитывать на то, что задачи УО с конечной областью определения могут решаться за время, меньшее экспоненциального. Существенно, однако, что в большинстве практических приложений алгоритмы УО общего назначения позволяют решать на несколько порядков величины более крупные задачи, чем рассмотренные ранее алгоритмы поиска.

В задачах, имеющих бесконечные области определения, отсутствует возможность описывать ограничения путем перечисления всех допустимых комбинаций значений и используется язык ограничений. Бесконечные области определения имеют дискретные переменные, например, множество всех целых чисел или множество всех строк. При решении задачкалендарного планирования строительных работ дата начала каждой работы представляет собой переменную, а ее возможными значениями являются целочисленные интервалы времени в сутках, отсчитываемых от текущей даты. Так, если работа Job₁ занимает n дней и должна предшествовать работе Job₃, то для описания этого условия применяется язык ограничений в виде алгебраического неравенства: StartJob₁ + n £ StartJob₃. Такие ограничения, однако, затруднительно преодолеть простым перечислением всех возможных присвоений, количество которых может быть большим. Для линейных ограничений с целочисленными переменными, подобных только что приведенному алгебраическому неравенству, существуют алгоритмы поиска решений, которые здесь не рассматриваются. До настоящего времени не известны алгоритмы поиска решений для нелинейных ограничений с целочисленными переменными. В отдельных случаях задачи с целочисленными ограничениями можно свести к задачам с конечной областью определения, например, при планировании можно установить верхний предел, равный общей продолжительности всех работ.

Часто встречаются и интенсивно изучаются задачи с непрерывными областями ограничений. Например, при планировании экспериментов на космическом телескопе необходимо предусматривать очень точную привязку экспериментальных наблюдений по времени. Начало и окончание каждого наблюдения и каждого маневра представляют собой переменные со значениями из непрерывной области определения, которые подчиняются всевозможным ограничениям, связанным с предысторией астрономического эксперимента и параметрами системы ориентации.

Кроме указания типов переменных, в задачах УО важно различать
типы ограничений. Эти ограничения могут быть унарными, бинарными и более высокого порядка, когда количество используемых переменных 2.

Все рассмотренные до сих пор ограничения являются абсолютными, их нарушение приводит к тому, что соответствующее решение больше не рассматривается как таковое. Кроме абсолютных ограничений, во многих реальных задачах УО применяются ограничения предпочтения, которые указывают, какие решения являются предпочтительными. Например, в задаче составления расписания занятий в университете часто учитывается, что профессор X предпочитает проводить занятия по утрам, а профессор Y – после полудня.