Квадратичные сравнения по составному модулю.
Рассмотрим сравнение вида x2≡a(mod pα), где p – простое нечетное число. Как было показано в п.4 §4, решение этого сравнения можно отыскать, решив сравнение x2≡a(mod p). Причем сравнение x2≡a(mod pα) будет иметь два решения, если a является квадратичным вычетом по модулю p.
Пример:
Решить квадратичное сравнение x2≡86(mod 125).
125 = 53, 5 – простое число. Проверим, является ли 86 квадратом по модулю 5.
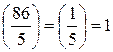 . Исходное сравнение имеет 2 решения.
. Исходное сравнение имеет 2 решения.
Найдем решение сравнения x2≡86(mod 5).
x2≡1(mod 5).
Это сравнение можно было бы решить способом, указанным в предыдущем пункте, но мы воспользуемся тем, что квадратный корень из 1 по любому модулю есть ±1, а сравнение имеет ровно два решения. Таким образом, решение сравнения по модулю 5 есть
x≡±1(mod 5) или, иначе, x=±(1+5t1).
Подставим получившееся решение в сравнение по модулю 52=25:
x2≡86(mod 25)
x2≡11(mod 25)
(1+5t1)2≡11(mod 25)
1+10 t1+25 t12≡11(mod 25)
10 t1≡10(mod 25)
2 t1≡2(mod 5)
t1≡1(mod 5), или, что то же самое, t1=1+5t2.
Тогда решение сравнения по модулю 25 есть x=±(1+5(1+5t2))=±(6+25t2). Подставим получившееся решение в сравнение по модулю 53=125:
x2≡86(mod 125)
(6+25t2)2≡86(mod 125)
36+12·25t2+625t22≡86(mod 125)
12·25t2≡50(mod 125)
12t2≡2(mod 5)
2t2≡2(mod 5)
t2≡1(mod 5), или t2=1+5t3.
Тогда решение сравнения по модулю 125 есть x=±(6+25(1+5t3))=±(31+125t3).
Ответ: x≡±31(mod 125).
Рассмотрим теперь сравнение вида x2≡a(mod 2α). Такое сравнение не всегда имеет два решения. Для такого модуля возможны случаи:
1) α=1. Тогда сравнение имеет решение только тогда, когда a≡1(mod 2), и решением будет x≡1(mod 2) (одно решение).
2) α=2. Сравнение имеет решения только тогда, когда a≡1(mod 4), и решением будет x≡±1(mod 4) (два решения).
3) α≥3. Сравнение имеет решения только тогда, когда a≡1(mod 8), и таких решений будет четыре. Сравнение x2≡a(mod 2α) при α≥3 решается так же, как сравнения вида x2≡a(mod pα), только в качестве начального решения выступают решения по модулю 8: x≡±1(mod 8) и x≡±3(mod 8). Их следует подставить в сравнение по модулю 16, затем по модулю 32 и т. д. вплоть до модуля 2α.
Пример:
Решить сравнение x2≡33(mod 64)
64=26. Проверим, имеет ли исходное сравнение решения. 33≡1(mod 8), значит сравнение имеет 4 решения.
По модулю 8 эти решения будут: x≡±1(mod 8) и x≡±3(mod 8), что можно представить как x=±(1+4t1). Подставим это выражение в сравнение по модулю 16
x2≡33(mod 16)
(1+4t1)2≡1(mod 16)
1+8t1+16t12≡1(mod 16)
8t1≡0 (mod 16)
t1≡0 (mod 2)
Тогда решение примет вид x=±(1+4t1)=±(1+4(0+2t2))=±(1+8t2). Подставим получившееся решение в сравнение по модулю 32:
x2≡33(mod 32)
(1+8t2)2≡1(mod 32)
1+16t2+64t22≡1(mod 32)
16t2≡0 (mod 32)
t2≡0 (mod 2)
Тогда решение примет вид x=±(1+8t2) =±(1+8(0+2t3)) =±(1+16t3). Подставим получившееся решение в сравнение по модулю 64:
x2≡33(mod 64)
(1+16t3)2≡33(mod 64)
1+32t3+256t32≡33(mod 64)
32t3≡32 (mod 64)
t3≡1 (mod 2)
Тогда решение примет вид x=±(1+16t3) =±(1+16(1+2t4)) =±(17+32t4). Итак, по модулю 64 исходное сравнение имеет четыре решения: x≡±17(mod 64)и x≡±49(mod 64).
Теперь рассмотрим сравнение общего вида: x2≡a(mod m), (a,m)=1,  - каноническое разложение модуля m. Согласно Теореме из п.4 §4, данному сравнению равносильна система
- каноническое разложение модуля m. Согласно Теореме из п.4 §4, данному сравнению равносильна система
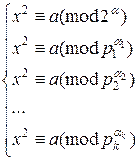
Если каждое сравнение этой системы разрешимо, то разрешима и вся система. Найдя решение каждого сравнения этой системы, мы получим систему сравнений первой степени, решив которую по китайской теореме об остатках, получим решение исходного сравнения. При этом количество различных решений исходного сравнения (если оно разрешимо) есть 2k, если α=1, 2k+1, если α=2, 2k+2, если α≥3.
Пример:
Решить сравнение x2≡4(mod 21).
21 – составное число. Факторизуем его: 21=3·7. Проверим разрешимость исходного сравнения:
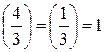 ,
, 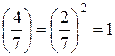 . Сравнение разрешимо и имеет 22=4 решения.
. Сравнение разрешимо и имеет 22=4 решения.
Составим систему: 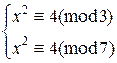 . Решим каждое из уравнений этой системы. Получим
. Решим каждое из уравнений этой системы. Получим 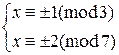 . Итак, имеем 4 системы:
. Итак, имеем 4 системы:
1)  2)
2) 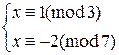 3)
3) 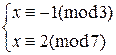 4)
4) 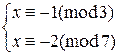
Решая каждую из этих систем по китайской теореме об остатках, получим четыре решения: x≡±2(mod 21), x≡±5(mod 21).
Дата добавления: 2015-11-28; просмотров: 5779;
