Тест на простоту Миллера-Рабина.

Теперь, наконец, мы располагаем достаточной информацией для того, чтобы привести тест Миллера-Рабина. Этот тест, как и тесты Ферма и Соловея-Штрассена, строит вероятно простые числа, то есть число, опознанное этим тестом как простое, может с некоторой малой вероятностью оказаться составным, однако вероятность ошибки у теста Миллера-Рабина гораздо ниже, чем у первых двух тестов. Как правило, для опознания простого числа достаточно одной итерации теста, но все же рекомендуемое количество итераций – пять.

Тест Миллера-Рабина основан на двух важных фактах:

1) Согласно теореме Ферма, если n – простое число, то для любого a: 0<a<n выполняется a^n—1≡1(mod n);

2) Если n – простое число, то сравнение x²≡1(mod n) имеет только тривиальные корни x≡±1(mod n), а если n – составное, то такое сравнение имеет несколько корней помимо тривиальных.

Тест Миллера-Рабина:

Вход: n=2^sr+1 – нечетное число, проверяемое на простоту, s≥0, r – нечетное.

t - количество итераций, параметр надежности.

1. Повторить t раз следующие шаги:

1.1. Случайным образом выбрать a: 1<a<n—1.

1.2. Строим последовательность b₀, b₁,…,b_s, где b_j= 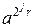mod n, j=0,1,…,s.

1.3. Если в построенной последовательности не встретилась «1», то идти на Выход с сообщением «n - составное число».

1.4. Если перед первой единицей в последовательности стоит не «-1», то идти на Выход с сообщением «n - составное число».

2. Идти на Выход с сообщением «n – простое число с вероятностью ε^t».

Выход.

Обратим внимание на то, что в последовательности b₀, b₁,…,b_s каждый последующий член является квадратом предыдущего по модулю n, а последний член есть ни что иное как a^n—1 mod n.

Вероятность ошибки ε ≤ φ(n)/4n, то есть верхняя граница ошибки на одной итерации для теста Миллера-Рабина в 2 раза меньше аналогичной для теста Соловея-Штрассена и в 4 раза – для теста Ферма.

Пример 1.

n=65=64+1=2⁶+1. r=1, s=6.

t=5.

1. 1-я итерация:

1.1. a=8.

1.2. Составляем последовательность: 8, 64=—1, 1, 1, 1, 1.

1.3. В последовательности встретилась «1».

1.4. Перед первой единицей стоит —1.

1. 2-я итерация:

1.1. a=11.

1.2. Составляем последовательность: 11, 56, 16, 61, 16, 61.

1.3. В последовательности не встретилась «1».

Выход: « n - составное число».

В том случае, когда тест Миллера-Рабина определяет составность числа n на шаге 1.4, появляется возможность частично факторизовать n.

Действительно, пусть в последовательности b₀, b₁,…,b_s, где b_j= 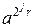mod n, нашлось такое i, что b_i≠±1, b_i+1=1. Обозначим для краткости b_i=b. Тогда b_i+1=b²≡1(mod n). Тогда n\(b²—1) n\(b+1)(b—1). Но в силу того, что b ±1(mod n), n не делит (b+1), n не делит (b—1). Следовательно,

1<НОД(n, b—1)<n,1<НОД(n, b+1)<n.

Значит, НОД(n,b—1) и НОД(n,b+1) являются нетривиальными делителями числа n.

Пример 2

n=161=160+1=2⁵·5+1. r=5, s=5.

1. 1-я итерация:

1.1. a=22. a⁵ mod 161 = 22⁵ mod 161=22.

1.2. Составляем последовательность: 22, 1, 1, 1, 1, 1.

1.3. В последовательности встретилась «1».

1.4. Перед первой единицей стоит 22.

Выход: « n - составное число».

Факторизуем 161: b=22. b+1=23, b—1=21.

Вычислим НОД(161, 23): 161=23·7+0.

НОД(161,21): 161=21·7+14

21=14·1+7

14=7·2+0.

Итак, нашли два нетривиальных делителя 161, и получили 161=23·7.

Надо заметить, что на самом деле случай, когда в тесте Миллера-Рабина возникает возможность факторизации, происходит весьма редко. Гораздо чаще сообщение о составности мы получаем на шаге 1.3.