Связь задач извлечения квадратных корней и факторизации по модулю RSA. Криптосистема Рабина.

Пусть дано сравнение x²≡a(mod pq), p, q – различные большие простые числа. Как следует из предыдущего пункта, решение данного сравнения можно найти, решив систему 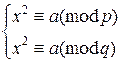, при этом необходимым условием существования решения является 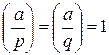. В том случае, если решения существуют, исходное сравнение имеет четыре различных решения: x≡±x₁(mod pq), x≡±x₂(mod pq)

Утверждение.

Для модуля RSA (n=pq, p, q – различные большие простые числа) задачи факторизации и извлечения квадратных корней вычислительно эквивалентны.

(Напомним, что две проблемы называются вычислительно эквивалентными, если за полиномиальное время по решению одной из них находится решение другой и наоборот.)

Доказательство:

1) Действительно, если умеем факторизовать модуль, то сможем извлечь квадратные корни по этому модулю (разложив исходное сравнение в систему и решив ее за полиномиальное время).

2) Если же разложения модуля RSA на простые сомножители неизвестно, но известны 4 различных решения сравнения x²≡a(mod n), и эти решения суть ±x(mod n), ±y(mod n). Выберем пару чисел x, y. Заметим, что x²≡y²(mod pq), x 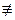±y(mod pq).

x²≡y²(mod pq) 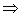x²—y² =(x+y)(x—y)≡0 (mod pq), причем x+y 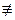0(mod pq),

x—y 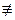0(mod pq). То есть pq\(x+y)(x—y), но pq не делит x+y, pq не делит x—y. Пользуясь основным свойствам простых чисел а также в силу равноправия сомножителей p и q, заключаем, что p\(x+y), q\(x—y), и тогда

p=НОД(x+y, n)

q=НОД(x—y, n).

Вычисление наибольшего общего делителя осуществляется при помощи полиномиального алгоритма – алгоритма Евклида.

□

Доказуемо стойкая криптосистема Рабина.

Криптосистема Рабина является асимметричной системой. Ее параметрами являются n=pq, p, q – различные большие простые числа. В качестве открытого ключа (ключа шифрования) выступает k₁=n, в качестве секретного ключа (ключа расшифрования) – k₂=(p,q).

Открытый текст x≠0 возводится в квадрат по модулю n, и получается криптограмма y=x² mod n. Для расшифрования последней требуется вычислить квадратный корень из y по модулю n. При решении сравнения y≡x² (mod n) возникнет четыре различных корня. Для того чтобы получатель мог выбирать нужный корень, в открытый текст x до шифрования вносится избыточность – участок текста определенного вида.

Для дешифрования криптограммы, то есть для вычисления x по y в отсутствие закрытого ключа требуется извлечь квадратный корень по составному модулю, не зная его разложения на простые сомножители.

Криптосистема называется доказуемо стойкой, если для нее доказана невозможность дешифрования без решения вычислительно трудной задачи. В силу доказанной вычислительной эквивалентности задач факторизации и извлечения квадратных корней, задача извлечения квадратных корней так же сложна, как задача факторизации, а последняя считается вычислительно сложной задачей. Поэтому криптосистема Рабина – доказуемо стойкая.