Жидкостно-газовые струйные аппараты

В таких аппаратах рабочий (жидкость) и пассивный (газ) потоки находятся в разных агрегатных состояниях, почти не изменяющихся в процессе смешения. В силу большой разницы плотностей взаимодействующих сред массовый коэффициент инжекции имеет величину порядка 10^–5, а объемный коэффициент инжекции 0,2–3,0.

В зависимости от типа струи различают жидкостно-газовые аппараты с компактной и с диспергированной струей. В зависимости от соотношения температур рабочей и пассивной сред рассматриваемые аппараты разделяют также на две группы: термодинамическую, в которой смешиваемые потоки имеют существенно разные температуры, и изотермическую, когда разница температур незначительна и ею можно пренебречь при расчете гидравлических процессов эжектирования.

В большинстве случаев аппараты с компактной струей относятся к изотермической группе. Наряду с традиционной формой проточной части (рис. 4.1, а) применяются ЖГСА, в которых рабочая жидкость подается в камеру смешения через несколько рабочих сопел или одно сопло (многоструйное, рис. 4.1, г) с несколькими отверстиями (многоструйное сопло). Увеличение поверхности контакта фаз взаимодействующих сред приводит к увеличению коэффициента инжекции при прочих равных условиях. Эффективность ЖГСА возрастает также в случае увеличения длины камеры смешения до 40–50 вместо 8–10 калибров для однофазных СА. Это связано с тем, что образование однородной газо-жидкостной эмульсии требует большей длины пути перемешивания, чем выравнивание профиля скорости однофазного потока. В этом случае отпадает необходимость в диффузоре.

ЖГСА с диспергированной струей в качестве рабочего сопла используют различные распылители жидкости (форсунки). Эти аппараты нашли широкое применение в химической, микробиологической, пищевой промышленности, системах очистки воды [34–36].

Расчет ЖГСА.Существующие методики расчета ЖГСА (все они разработаны для водовоздушных эжекторов, применяемых в основном в энергетике как вакуумные струйные насосы) являются эмпирическими, справедливыми в достаточно узком диапазоне режимных и конструктивных параметров. Анализ этих методик выполнен в [18].

Течение в камере смешения представляется следующим образом. Струя жидкости поступает в камеру смешения, сохраняя свою первоначальную цилиндрическую форму. Примерно на расстоянии 2 – 3 калибров d₃ от начала камера смешения оказывается заполненной молочно-белой водовоздушной эмульсией (пеной), причем у стенок камеры смешения наблюдаются обратные токи водовоздушной эмульсии, которая снова захватывается струей и увлекается ею. Это возвратное движение обусловлено повышением давления по длине камеры смешения. Давление р_н в начале камеры смешения равно давлению в приемной камере. При низких противодавлениях повышение давления в цилиндрической камере смешения сравнительно невелико. Основное повышение давления происходит в диффузоре. При увеличении противодавления эта картина изменяется: степень повышение повышения давления в диффузоре уменьшается, а в камере смешения — резко увеличивается, причем оно это происходит на сравнительно небольшом участке камеры смешения скачкообразно. Чем меньше отношение 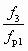, тем более резко выражен скачок давления. Место скачка хорошо различимо, т. к. после него движется уже не молочно-белая эмульсия, а прозрачная вода с пузырьками воздуха.

Чем больше отношение 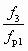, тем более развиты обратные токи водовоздушной эмульсии. С увеличением противодавления скачок давления перемещается против течения струи и, наконец, при определенном противодавлении (р_с)_max достигает начала камеры смешения. При этом эжекция воздуха водой прекращается, вся камера смешения заполнена прозрачной водой без пузырьков воздуха. Аналогичные явления имеют место, если при неизменном противодавлении снижается давление рабочей воды перед соплом.

Согласно [14], отношение объемных расходов инжектируемой и рабочей сред сохраняется достаточно стабильным при изменении в широких пределах параметров его работы (p_p, p_н, р_с и G_р). Поэтому, в отличие от рассмотренных выше СА, в ряде методик расчета используются объемные коэффициенты инжекции (подсоса) по паровоздушной смеси и сухому воздуху:

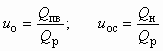, (8.1)

где Q_пв, Q_н и Q_р — объемные расходы соответственно инжектируемой (паровоздушной), воздушной и рабочей (жидкостной) сред, м³/с.

В камере смешения происходит насыщение воздуха парами воды. Температура пара в эмульсии практически равна температуре воды T_p. Поэтому газовая фаза эмульсии представляет собой насыщенную паровоздушную смесь, полное давление которой в начале камеры смешения равно давлению инжектируемого сухого воздуха в приемной камере р_н. Парциальное давление воздуха р_в в смеси меньше этого давления на давление насыщенного пара р_нп при температуре рабочей жидкости T_p, т. е. р_в = р_н – р_нп.

Поскольку сжимаемый в СА воздух входит в состав паровоздушной смеси, то Q_пв в (8.1) представляет собой объемный расход паровоздушной смеси. Воспользовавшись законом Дальтона и уравнением Менделеева — Клайперона, нетрудно выразить массовый расход инжектируемого сухого воздуха в виде

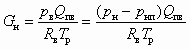. (8.2)

Тот же расход ,можно выраженныйзить через параметры инжектируемого сухого воздуха:

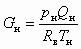, (8.3)

где Q_н, T_н — объемный расход и абсолютная температура сухого воздуха на всасывании.

Из этих уравнений нетрудно установить взаимосвязь между u_o и u_oс

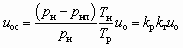, (8.4)

где 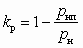; k_т = T_н/T_p.

В случае р_н > р_нп и T_н » T_р имеем u_oс » u_o.

При G_н = 0 (u_oс = 0) р_н = р_нп, т. е. давление всасывания равно давлению насыщенного пара при температуре рабочей воды T_р. Несмотря на равенство u_oс = 0 u_o  0, т. к. в приемной камере эжектора происходит вскипание рабочей воды и выделившийся пар отсасывается этой же рабочей водой.

Для расчета ЖГСА с компактной струей и короткой цилиндрической камерой смешения (длиной около 10 калибров) можно воспользоваться формулами для СН.

Если предположить одинаковые удельные объемы рабочей и сжатой сред, скорость эжектируемой среды равной нулю, то после замены массового коэффициента инжекции u объемным u_o будем иметь следующие уравнения, определяющие:

- достижимый объемный коэффициент инжекции

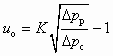, (8.5)

где K — эмпирический коэффициент (для водовоздушного СА равный 0,85); D р_р = р_р – р_н — располагаемый перепад давления рабочей воды; Δр_с = р_с – р_н — перепад давления, создаваемый эжектором;

- отношение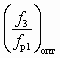

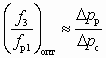; (6.3.8.6)

- характеристику ЖГСА, аналогичную СН (см. уравнение (6.1) при условии р₂ = р_н, чему отвечает f_н2 = ¥ и, соответственно, ))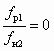

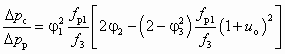. (8.7)

Уравнение (8.7) может быть представлено в следующей модификации

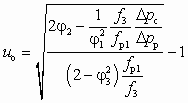, (8.8)

которой удобно пользоваться для определения объемного коэффициента инжекции ЖГСА по заданным отношениям сечений 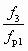и перепадов давлений .

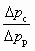Из уравнения (8.8) следует, что для аппарата данных размеров 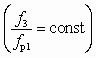в области глубокого вакуума, когда при постоянных значениях р_р и р_с существенные изменения р_н практически не меняют отношения 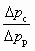, объемный коэффициент инжекции остается постоянным. Поскольку при этом расход рабочей воды практически не меняется, то и объемный расход паровоздушной смеси также остается постоянным.

Наряду с изложенной предлагаются и другие методики расчета ЖГСА с короткой камерой смешения, приведенные в [15, 18].

В [14] содержится информация для расчета ЖГСА с удлиненной цилиндрической камерой смешения, а также многоструйного ЖГСА.

Методы расчета ЖГСА с диспергированной струей, как и других типов гидроструйных аппаратов, основываются также на эмпирических или полуэмпирических моделях. Законченной теории расчета в настоящее время нет.

Несмотря на большую работу по исследованию СА, эффективность ЖГСА осталась на уровне, достигнутом в 1920-е годыг., что объясняется сложностью внутренних процессов в ЖГСА и их недостаточной изученностью. Поэтому весьма важной задачей является дальнейшее изучение механизма рабочего процесса ЖГСА с целью разработки более строгой методики расчета.

Очевидно, что эмпирический подход к решению этой задачи малоперспективен.

Полуэмпирический подход, включающий в себя ту или иную физико-математическая математическую модель с разной степенью приближения к реальному физическому процессу, которая затем коррелируется эмпирическими данными, более перспективен.

В этой связи отметим работу [37], в которой Достаточно успешно в рамках теории взаимопроникающих континуумов осуществлено моделирование гидродинамики в ЖГСА с диспергированными и компактными струями в [37].