Струйные однофазные насосы
Уравнение характеристики струйных насосов (СН или СОН, см. рис. 5.1, д), согласно [14], имеет вид
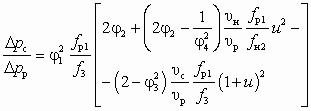 , (6.1)
, (6.1)
где 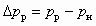 ;
; 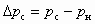 ;
; 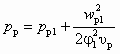 ;
;
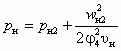 ;
; 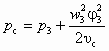 ;
; 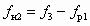 ;
;
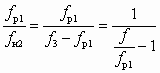 .
.
Уравнение (6.1) — результат применения теоремы об изменении количества движения для цилиндрической камеры смешения (см. рис. 4.3, б) с использованием коэффициентов j1, j2, j3 и j4, названных коэффициентами скорости сопла, камеры смешения, диффузора и входного участка камеры смешения (конфузора). Основное допущение при выводе — это неизменность сечения рабочего потока, т. е. fp1 = fp2 = idem. Значения коэффициентов j1, j2, j3 и j4 рекомендуется принимать [14] соответственно 0,95; 0,975; 0,9 и 0,925.
При расчете высоконапорных СН, характеризующихся отношением 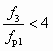 , уравнение (6.1) дает завышенную величину
, уравнение (6.1) дает завышенную величину 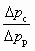 в области повышенных значений u. Поэтому расчет таких СН должен проводиться по более точному уравнению (6.2), учитывающему изменение сечения рабочего потока на входном участке камеры смешения ( fp2 fp1), вызванное снижением статического давления на этом участке (р2 = рр2 = рн2 рн):
в области повышенных значений u. Поэтому расчет таких СН должен проводиться по более точному уравнению (6.2), учитывающему изменение сечения рабочего потока на входном участке камеры смешения ( fp2 fp1), вызванное снижением статического давления на этом участке (р2 = рр2 = рн2 рн):
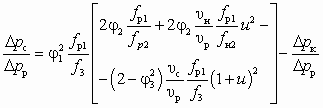 , (6.2)
, (6.2)
где Dрк = рн – р2 — снижение статического давления на входном участке камеры смешения; р2 = рр2 = рн2 — статическое давление во входном сечении камеры смешения;
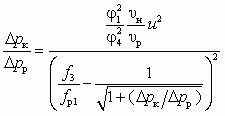 ; (6.3)
; (6.3)
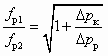 ; (6.4)
; (6.4)
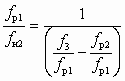 . (6.5)
. (6.5)
Как следует из анализа соотношений (6.3)–(6.5), отношения сеченийвеличины 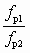 и
и 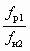 являются величинами переменными, зависящими от u. Характер зависимости показан на рис. 6.1.
являются величинами переменными, зависящими от u. Характер зависимости показан на рис. 6.1.
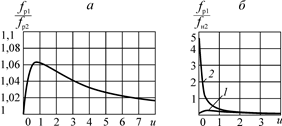
Рис. 6.1. Зависимости 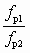 (а) и
(а) и 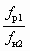 (б) от u:
(б) от u:
1 — без учета снижения статического давления;
2 — с учетом снижения статического давления
При расчете характеристики по уравнению (6.3.6.2) следует предварительно для каждого значения u найти любым численным методом 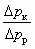 , а затем
, а затем 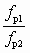 и
и 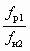 .
.
Совершенство струйного насоса (СН) определяется величиной КПД. В применении к СН выражение (5.38) преобразуется к виду:
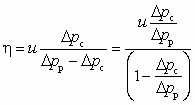 . (6.6)
. (6.6)
Определение достижимых параметров и оптимального отношения сечений 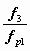
При заданных величинах Dрр и u оптимальное отношение сечений 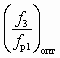 соответствует максимальному значению перепада давлений Dрс, развиваемого СН, и поэтому находится аналогично СА для пневмотранспорта зернистых материалов:
соответствует максимальному значению перепада давлений Dрс, развиваемого СН, и поэтому находится аналогично СА для пневмотранспорта зернистых материалов:
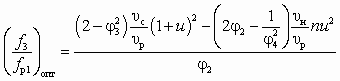 , (6.7)
, (6.7)
где
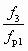
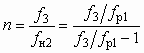 . (6.8)
. (6.8)
Из совместного решения (6.7)–(6.8) следует зависимость для однозначного определения 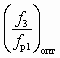 :
:
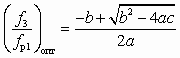 , (6.9)
, (6.9)
где
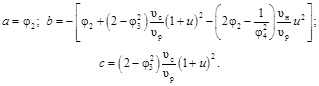
При подстановке 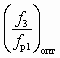 в (6.1) находят достижимый перепад давлений D рс.
в (6.1) находят достижимый перепад давлений D рс.
Совместное решение (6.7) и (6.1) дает зависимость для непосредственного расчета достижимого относительного перепада давлений СН без необходимости предварительного расчета 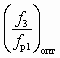 :
:
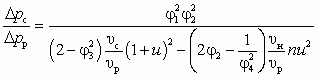 . (6.10)
. (6.10)
Характер зависимостей достижимых параметров 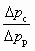 ,
, 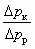 , h при
, h при 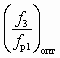 и
и 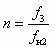 для каждого значения u представлен на рис. 6.2, что позволяет осуществить приближенный выбор СН.
для каждого значения u представлен на рис. 6.2, что позволяет осуществить приближенный выбор СН.
Если задан Dрс, а искомой величиной является достижимый коэффициент инжекции u, то, предварительно определив из совместного решения (6.7) и (6.10)
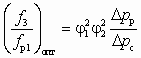 , (6.3.6.11)
, (6.3.6.11)
а также n из (6.8), после преобразований (6.10) нетрудно получить
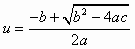 ,
,
где 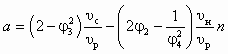 ;
;
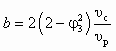 ;
;
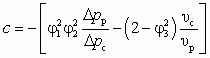 .
.
На рис. 6.3 показана расчетная кривая достижимых параметров 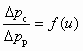 , построенная с помощью (6.9) и (6.10). Там же приведены характеристики СН с различным отношением
, построенная с помощью (6.9) и (6.10). Там же приведены характеристики СН с различным отношением 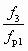 . Как видно из рис. 6.3, кривая оптимальных параметров является огибающей семейства характеристик СН с различным отношением
. Как видно из рис. 6.3, кривая оптимальных параметров является огибающей семейства характеристик СН с различным отношением 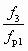 и касается этих характеристик в точках, соответствующих оптимальным режимам их работы.
и касается этих характеристик в точках, соответствующих оптимальным режимам их работы.
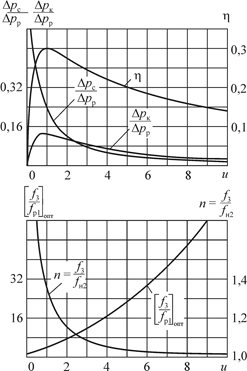
Рис. 6.2.Зависимость  ,
, 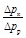 ,
, 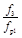 , n и h от коэффициента инжекции u струйного насоса
, n и h от коэффициента инжекции u струйного насоса
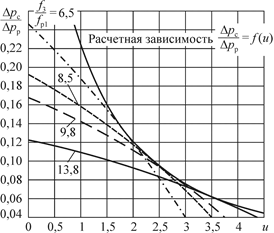
Рис. 6.3. Характеристики СН 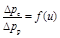 при различных
при различных 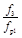
Дата добавления: 2016-01-20; просмотров: 816;
