Асимптоты графика функции
При исследовании функций часто бывает, что при удалении координаты х точки кривой на бесконечность кривая неограниченно приближается к некоторой прямой.
Определение. Прямая называется асимптотойкривой, если расстояние от переменной точки кривой до этой прямой стремится к нулю при удалении этой точки на бесконечность.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции 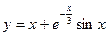 . Ее наклонная асимптота
. Ее наклонная асимптота 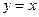 .
.
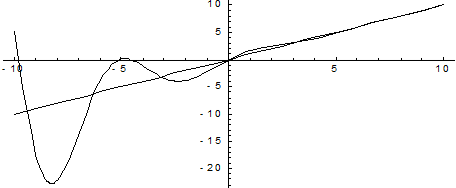
Вертикальные асимптоты.
Из определения асимптоты следует, что если 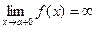 или
или 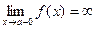 или
или 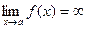 , то прямая
, то прямая 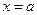 – асимптота кривой
– асимптота кривой 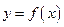 .
.
Например, для функции 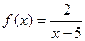 прямая
прямая 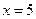 является вертикальной асимптотой.
является вертикальной асимптотой.
Наклонные асимптоты.
Предположим, что кривая 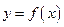 имеет наклонную асимптоту
имеет наклонную асимптоту 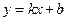 .
.
 M
M

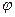
N
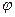 P
P
Q
Обозначим точку пересечения кривой и перпендикуляра к асимптоте через М. Пусть Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью 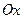 обозначим
обозначим 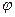 . Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда
. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда 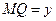 – ордината точки кривой,
– ордината точки кривой, 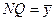 - ордината точки N асимптоты.
- ордината точки N асимптоты.
По условию: 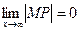 ,
, 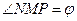 ,
, 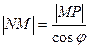 . Угол
. Угол 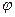 - постоянный и не равен
- постоянный и не равен 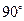 . Следовательно,
. Следовательно,
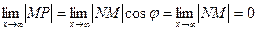 ,
,
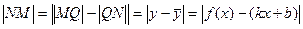 .
.
Тогда 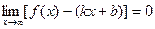 .
.
Следовательно, прямая 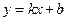 – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов
– асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов 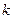 и
и 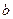 .
.
В полученном выражении выносим за скобки  :
:
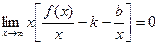 .
.
Так как 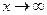 , то
, то 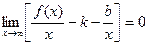 , т.к.
, т.к. 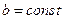 , то
, то 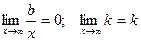 .
.
Тогда 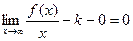 . Следовательно,
. Следовательно,
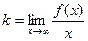 .
.
Так как 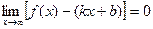 , то
, то 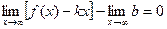 . Следовательно,
. Следовательно,
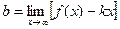
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при 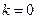 .
.
Пример. Найти асимптоты и построить график функции 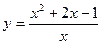 .
.
1) Вертикальные асимптоты: 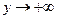
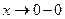 :
: 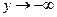
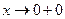 . Следовательно,
. Следовательно, 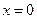 - вертикальная асимптота.
- вертикальная асимптота.
2) Наклонные асимптоты:
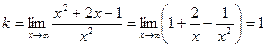 ,
,
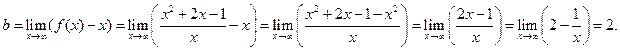 Таким образом, прямая
Таким образом, прямая 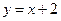 является наклонной асимптотой графика функции. Построим график функции.
является наклонной асимптотой графика функции. Построим график функции.
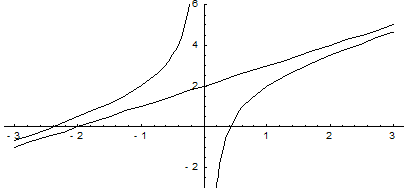
Пример. Найти асимптоты и построить график функции 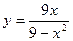 .
.
Прямые 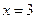 и
и 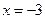 являются вертикальными асимптотами кривой.
являются вертикальными асимптотами кривой.
Найдем наклонные асимптоты:
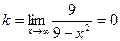 ,
, 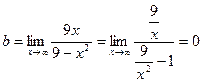
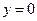 – горизонтальная асимптота. Построим график функции.
– горизонтальная асимптота. Построим график функции.
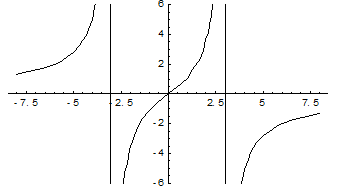
Пример. Найти асимптоты и построить график функции 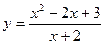 .
.
Прямая 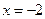 является вертикальной асимптотой кривой.
является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.
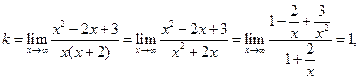
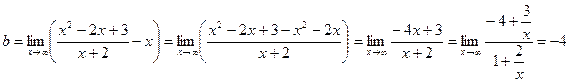 .
.
Следовательно, прямая 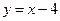 является наклонной асимптотой. Построим график функции.
является наклонной асимптотой. Построим график функции.
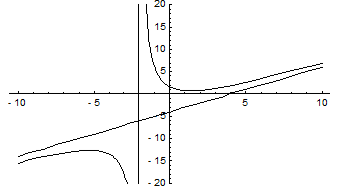
Дата добавления: 2015-11-28; просмотров: 2037;
