Условия перехода ламинарного течения жидкости в турбулентное

Характер течения жидкости - ламинарный или турбулентный - за­виситот плотности жидкости r, ее вязкости h , скорости течения v , диаметра трубы d, по которой течет жидкость. Оказывается, что не­которая комбинация этих величин - один безразмерный параметр - мо­жет определять условия перехода ламинарного течения жидкости в турбулентное. Таким параметром является число Рейнольдса (Re) :

Re = 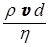. (26)

Когда число Рейнольдса не превышает некоторого критического значения Re_кр ,течение жидкости ламинарно. Если же Re > Re_кр , то в потоке жидкости возникают завихрения - ее течение становится тур­булентным.

Значение критического числа Рейнольдса можно определить экс­периментально. Представим, что по гладкой цилиндрической трубе протекает вода с регулируемой и измеряемой скоростью v, которая представляет собой среднюю по сечению трубы скорость течения. Плотность воды, ее вязкость и диаметр трубы известны. Допустим, что труба прозрачна и переход течения жидкости из ламинарного в турбулентное можно определить визуально. Постепенно увеличивая скорость течения, отметим то ее значение v_кр, при котором в потоке жидкости начинает проявляться турбулентность. Подставив это значе­ние v_кр в формулу (26), получим величину критического числа Рей­нольдса. Для гладких труб Re_кр = 2300.

Если Re_кр известно, то становится возможным для любой жидкос­ти и разных условий ее течения предсказать, будет ли ее поток ла­минарным или турбулентным.

Пример. Вода течет по трубе диаметром d = 2 мм. При какой скорости v ее течение становится турбулентным?

Примем вязкость воды h = 10^-3 Па×с, плотность r = 10³ кг/м³ и подставим эти значения в правую часть формулы (26). В левую часть подставим значение критического числа Рейнольдса. Из образовавше­гося уравнения: 2300 = v×10³×2×10^-3/10^-3, найдем, что течение воды в этой трубе становится турбулентным при скорости
v = 1,15 м/с. С увеличением диаметра трубы и уменьшением вязкости жидкости переход из ламинарного течения в турбулентное наступает при уменьшающихся значениях скорости.

Движение крови в организме, в основном, ламинарно. Однако, при определенных условиях кровоток может приобретать и турбулент­ный характер. Анализ формулы (26) позволяет предсказать эти усло­вия. Действительно, турбулентности могут проявляться в полостях сердца (велико значение d). По-видимому, их наличие здесь физиоло­гически целесообразно, поскольку возникающие завихрения приводят к более равномерному перемешиванию порций крови, поступавших из ма­лого круга кровообращения в левый желудочек сердца и, следователь­но, способствует более равномерному обогащению кислородом объема крови, выталкиваемой в большой круг кровообращения. Сравнительно небольшие завихрения могут возникать в аорте и вблизи клапанов сердца (здесь, ведь, велико и значение скорости движения крови).

При интенсивной физической нагрузке скорость движения крови увеличивается и это может вызвать турбулентности в кровотоке.

Из формулы (26) следует также, что с уменьшением вязкости турбулентный характер течения жидкости может проявляться и при сравнительно небольшой скорости ее движения. Поэтому, при некото­рых патологических процессах, приводящих к аномальному снижению вязкости крови, кровоток в крупных кровеносных сосудах может стать турбулентным.

Следует иметь в виду, что значение критического числа Рей­нольдса 2300 приведено для гладких труб и ньютоновской жидкости. Реальная кровь условию однородности не соответствует, поэтому Re_кр для крови имеет меньшее значение и по различным литературным дан­ным составляет около 1600 - 900. Кроме того, кровеносный сосуд в ряде случаев нельзя моделировать гладкой трубой. В частности, при наличии атеросклеротических бляшек в просвете сосудов имеются ло­кальные сужения, приводящие к возникновению турбулентности в тече­нии крови. Наличие турбулентности в кровотоке может быть обнаружено по шумам, прослушиваемым с помощью фонендоскопа.

Турбулентное течение крови по сосудам создает повышенную наг­рузку на сердце, что способствует развитию патологических процес­сов в сердечно-сосудистой системе.