Течение вязкой жидкости. Формула Пуазейля

Занимаясь исследованием кровообращения, французский врач и физик Пуазейль пришел к необходимости количественного описания процессов течения вязкой жидкости вообще. Установленные им для этого случая закономерности имеют важное значение для понимания сущности гемодинамических явлений и их количественного описания. Не производя строгих математических расчетов, проанализируем, от чего зависит объем V вязкой жидкости, ламинарно протекающей по участку гладкой трубы длиной L и радиусом r (рис. 11). Очевидно, этот объем будет прямо пропорционален времени истечения жидкости t и тому перепаду давлений
Р₁ - Р₂, который обуславливает ток жидкости на участке трубы длиной L . Естественно, что объем вытекающей жид­кости будет резко возрастать и с увеличением площади поперечного сечения рассматриваемого участка. Теоретические расчеты и непос­редственный эксперимент показывают, что V ~ r ⁴ . Помехой истечению жидкости является ее вяз­кость h, поэтому объем V ~ 1/h . Чем больше длина участка, тем больше потери в скорости протекающей по нему жидкости, значит V ~ 1/L. Приведенные соображе­ния, строгое теоретическое рассмотрение и непосредс­твенный эксперимент приводят к формуле Пуазейля:

V = 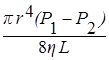t . (13)

Формулу (13) можно представить в более наглядном виде. Разделив обе части этого выражения на время истечения t, слева получим объ­емную скорость течения жидкости Q (см. раздел 1.2). Величину 8hL / p r⁴ обоз­начим через X. Тогда формула (13) принимает вид:

Q = 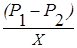. (14)

Такая запись формулы Пуазейля (ее еще называют уравнением Гаге­на-Пуазейля) аналогична закону Ома для участка электрической цепи.

Вообще, между законами гидродинамики и законами протекания электрического тока по электрическим цепям существует тесная ана­логия. Объемная скорость течения жидкости Q является гидродинами­ческим аналогом силы электрического тока I . Причиной прохождения электрического тока является разность электрических потенциалов j₁ - j₂ на соответствующем участке цепи. Гидродинамическим аналогом этой разности является перепад давлений Р₁ - Р₂ . Закон Ома: I = ( j₁ - j₂ ) / R, где R - электрическое сопротивление, имеет своим гид­родинамическим аналогом формулу (14), в которой величина X = 8hL/pr⁴ представляет собой гидравлическое сопротивление - аналог электри­ческого сопротивления R.

Если обратиться от общих законов истечения вязкой жидкости к задачам гемодинамики, то с помощью формулы Пуазейля можно опреде­лить ряд характеристик кровотока. Так, зная объемную скорость кровотока Q и величину гидравлического сопротивления сосудов, можно найти величину давления крови в любой точке сосудистой системы.

Если Р_о - давление крови в желудочке сердца, а X - общее сопро­тивление сосудов на участке сосудистой системы между желудочком и данной точкой, то давление крови Р в данной точке, согласно форму­ле (14) , равно:

Р = Р_о - QX . (15)

Гидравлическое сопротивление X разветвленного участка сосу­дистой системы может быть определено по аналогии с расчетом общего электрического сопротивления участка электрической цепи, состояще­го из набора отдельных резисторов. Для случая последовательно сое­диненных сосудов (см.рис.12а) общее сопротивление определяется суммой их отдельных гидравлических сопротивлений:

X = X₁ + X₂ + X₃ + ... + X_n . (16)

При параллельном ветвлении сосудистого русла (см.рис.12б) об­щее сопротивление находится из уравнения:

(17)

а) б)

Рис.12