Общая постановка задачи ДП

Модели динамического программирования

Динамическое программирование (ДП) применяется при решении оптимизационных задач, в которых процесс принятия решений может быть разбит на этапы (шаги).

Если модели линейного программирования (ЛП) применяются в экономике для принятия крупномасштабных плановых решений в сложных ситуациях, то модели ДП применяются при решении задач значительно меньшего масштаба, например, при разработке правил управления запасами, устанавливающими момент пополнения запасов, при распределении дефицитных капитальных вложений между возможными новыми направлениями их использования, при разработке долгосрочных правил замены выбывающих из эксплуатации основных фондов и т.д.

Общая постановка задачи ДП

Рассматривается управляемый процесс, например, экономический процесс распределения средств между предприятиями, распределения ресурсов в течение ряда лет и т.п. В результате управления система (объект управления) 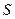переводится из начального состояния 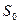в состояние 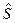. Предположим, что управление можно разбить на 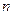шагов, т.е. 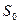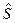решение принимается последовательно на каждом шаге, а управление, переводящее систему из в , можно представить в виде последовательности 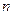пошаговых управлений.

Обозначим через 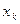управление на 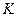-м шаге 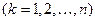. Переменные 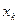удовлетворяют некоторым ограничениям и в этом смысле называются допустимыми.

Пусть 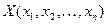- управление, переводящее систему 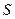из состояния 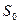в состояние .

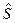Обозначим через 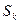- состояние системы после 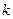-го шага управления.

Получаем последовательность состояний системы

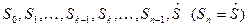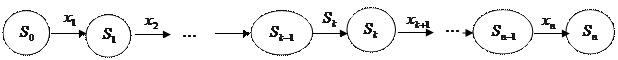
Показатель эффективности F управляемой операции (целевая функция) зависит от начального состояния и управления:

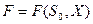(1)

Предположим, что:

1. Состояние системы в конце 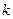-го шага зависит только от предшествующего состояния 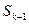и управления на 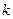-м шаге 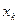и не зависит от других предшествующих состояний и управлений. Это положение записывается в виде уравнений

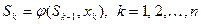(2),

которые называются уравнениями состояний.

2. Целевая функция 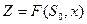является аддитивной: 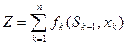(3),

где 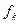- показатель эффективности каждого шага.

Задача ДП формулируется так:

Определить такое допустимое управление 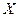, переводящее систему 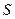из состояния 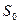в состояние 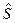, при котором целевая функция (3) принимает наибольшее (наименьшее) значение.

Особенности модели ДП.

1. Задача оптимизации интерпретируется как n-шаговый процесс управления.

2. Целевая функция (ЦФ) – сумма ЦФ на каждом шаге.

3. Выбор управления на к -ом шаге зависит только от состояния системы к этому шагу и не влияет на предшествующие шаги (нет обратной связи).

4. Состояние системы после к - го шага управления зависит от предшествующего состояния и управления.

5. На каждом шаге управление 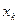зависит от конечного числа управляющих переменных, а состояние 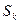- от конечного числа параметров.

Рассмотрим схему ДП, которая не зависит от способов задания функции и ограничений.