Классификация медицинской электронной аппаратуры 4 страница
Рис. 3.8
Обратный пьезоэффкт – появление механических деформаций под действием электрического поля. В УЗ-излучателях основной частью является пластина из сегнетоэлектрика (рис. 3.9). На поверхности этой пластины наносятся два слоя из электропроводящего материала - это два электрода на противоположных сторонах пластины. Если к электродам подать переменное
 электрическое напряжение, то пластина за счет обратного пьезоэффекта начинает вибрировать, излучая механическую волну соответствующей
электрическое напряжение, то пластина за счет обратного пьезоэффекта начинает вибрировать, излучая механическую волну соответствующей
| Рис. 3.9 | частоты |
УЗ оказывает на вещество сложное действие: механическое, физико-химическое и тепловое. На этом сложном действии основано биологическое действие УЗ, который может вызывать гибель вирусов, бактерий, грибков и т.п., а при значительной мощности даже и мелких животных. При незначительной мощности УЗ повышает проницаемость клеточных мембран, активизируя процессы обмена.
Поэтому УЗ применяют
1. В терапии – для прогревания: УЗ поглощается тканями, акустическая энергия преобразуется в тепловую.
2. В диагностике – УЗИ. Отражение УЗ на границе двух сред зависит от соотношения их волновых сопротивлений. УЗ хорошо отражается на границах мышца - надкостница – кость. Поэтому можно определить расположение и размер неоднородных включений, полостей, органов и т.п.
3. В хирургии - сварка и распиливание костей, создание отверстий в костях.
4. В лабораториях – для определения скорости кровотока с помощью эффекта Доплера.
Рассмотренные примеры не ограничивают область применения УЗ в медицине.
Лекция 4
Гидродинамика
Прежде, чем мы начнем изучать гемодинамику, т.е. закономерности кровообращения, мы должны рассмотреть механические свойства жидкостей вообще и закономерности их течения, т.е. изучить гидродинамику.
Свойства жидкостей
Свойства жидкостей являются промежуточными между свойствами газов и твердых тел.
1. Текучесть – свойство молекул жидкости относительно легко смещаться под действием внешних сил.
2. Проявление сил поверхностного натяжения на свободной поверхности жидкости.
3. Относительная несжимаемость, проявляющаяся в том, что объём жидкости практически не меняется под действием внешних сил, вызывающих её объёмное сжатие. Это связано с тем, что действие внешних сил компенсируется силами взаимного отталкивания между молекулами, которые в жидкости достаточно большие.
Хотя объём жидкости под действием внешних сил не меняется, жидкость при этом находится в напряженном состоянии, т.е. под давлением. Паскаль установил такой закон: “Вследствие подвижности частиц давление в жидкости передается равномерно во все стороны “. Это давление передается также на стенки сосуда, в котором находится жидкость, а также на тело, погруженное в жидкость
 .
.
4. Вязкость или внутреннее трение - проявляется в том, что взаимное смещение частиц жидкости сопровождается некоторым сопротивлением.
Основные понятия гидродинамики
Идеальная жидкость – жидкость, которая не сжимается и не имеет внутреннего трения.
Стационарное или установившееся течение – течение, при котором скорости течения жидкости в каждой точке потока со временем не изменяются.
Установившееся течение характеризуют линиями тока – это воображаемые линии, совпадающие с траекториями движения частиц. Часть потока жидкости, ограниченная со всех сторон линиями тока, образует трубку тока (струю).
Уравнение неразрывности струи
 В общем потоке жидкости выделим трубку тока настолько узкую, что скорость частиц в любом её сечении
В общем потоке жидкости выделим трубку тока настолько узкую, что скорость частиц в любом её сечении 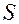 , перпендикулярном оси трубки, можно считать постоянной: в сечении
, перпендикулярном оси трубки, можно считать постоянной: в сечении  везде -
везде -  , в сечении
, в сечении 
| Рис. 4.1 | везде -  . .
|
При стационарном течении частицы движутся только по ли-ниям тока, поэтому боковую поверхность они не пересекают. Значит, жидкость движется только в трубке тока.
Если за время  в трубку тока вошел объём жидкости
в трубку тока вошел объём жидкости  , то такой же объём жидкости должен и выйти из неё. Через сечение
, то такой же объём жидкости должен и выйти из неё. Через сечение  за это время проходит объём
за это время проходит объём  , через сечение
, через сечение  объём
объём  .
.
Т.к.  , то
, то
 ,
,
т.е.  .
.
Это и есть уравнение неразрывности струи.
Из уравнения неразрывности струи следует:
 ,
,
т.е. чем больше площадь сечения, тем меньше скорость частиц.
Уравнение неразрывности струи выполняется и для реальной жидкости.
Уравнение Бернулли
Жидкость, находящаяся под давлением, обладает внутренней потенциальной энергией – энергией давления
 ,
,
где  – давление,
– давление,  – объём жидкости.
– объём жидкости.
 Пусть в трубке тока перемещается масса жидкости
Пусть в трубке тока перемещается масса жидкости  (рис. 4.2). Перемещение происходит под действием сил давления в сечениях
(рис. 4.2). Перемещение происходит под действием сил давления в сечениях  и
и  .
.
| Рис.2 | При этом совершается работа:
 ( (  ) )
|
Эта работа расходуется на преодоление действия сил тяжести, работа  , и на изменение кинетической энергии жидкости, работа
, и на изменение кинетической энергии жидкости, работа  :
:
 .
.
 ,
,
 .
.
Подставим уравнения (4.3), (4.5) и (4.6) в уравнение (4.4), получим

Перенесем слагаемые с индексом 1 в левую часть уравнения, а с индексом 2 – в правую:
 , т.е.
, т.е.
 .
.
Разделим на  все слагаемые уравнения и, помня, что
все слагаемые уравнения и, помня, что  , получим уравнение Бернулли
, получим уравнение Бернулли
 ,
,
где  статическое давление,
статическое давление,
 гидростатическое давление,
гидростатическое давление,
 - гидродинамическое давление.
- гидродинамическое давление.
Т.о. уравнение Бернулли следует читать так: полное давление жидкости, равное сумме статического, гидростатического и гидродинамического давлений, остается постоянным в любом сечении трубы.
Практические следствия из уравнения Бернулли.
1) Определение гидростатического давления
Если  но высота сечений над нулевым уровнем энергии различна
но высота сечений над нулевым уровнем энергии различна  и
и  , соответственно.
, соответственно.
 Тогда
Тогда  , его можно перенести в правую часть уравнения Бернулли и оно примет вид
, его можно перенести в правую часть уравнения Бернулли и оно примет вид

Откуда

Следовательно,  Δ.
Δ.
Рис. 4.3
 измеряем манометром,
измеряем манометром,  определяем перепад гидростатического давления на данном участке трубы.
определяем перепад гидростатического давления на данном участке трубы.
2) Правило Бернулли
Если взять трубу, имеющую различные сечения  и
и  , следовательно, скорости
, следовательно, скорости  и
и  также разные.
также разные.
 В горизонтальной трубе постоян-
В горизонтальной трубе постоян-
ным остается гидростатическое
давление, т.к. высота над нулевым
уровнем остается постоянной,
 . Поэтому уравнение Бернулли запишется как
. Поэтому уравнение Бернулли запишется как
 ,
,
| Рис. 4.4 | 
|
Отсюда следует вывод – правило Бернулли: статическое давление невязкой жидкости при сужении сосуда понижается, а при расширении увеличивается.
Действительно, из уравнения видно, что, если  , то должно быть
, то должно быть  чтобы полное давление не изменилось.
чтобы полное давление не изменилось.
3. Определение гидродинамического давления и скорости течения жидкости.

 гидростатическое давление, измеряемое прямой трубой.
гидростатическое давление, измеряемое прямой трубой.
 полное давление, измеряемое изогнутой трубой. Сечение трубы постоянное, труба горизонтальная. Следовательно, гидростатическое давление одинаково по всей
полное давление, измеряемое изогнутой трубой. Сечение трубы постоянное, труба горизонтальная. Следовательно, гидростатическое давление одинаково по всей
| Рис. 4.5 | трубе и измеряется обеими трубками. Поэтому |


Величину  измеряем, следовательно, определяем гидродинамическое давление, а затем определяем скорость течения жидкости как
измеряем, следовательно, определяем гидродинамическое давление, а затем определяем скорость течения жидкости как

4.Всасывающее действие струи – водоструйный насос.
Водоструйный насос представляет собой стеклянный сосуд, в который впаяно три трубки (Рис 3.6). Трубка 1, в конце которой имеется коническое сужение, соединяется с водопроводом. Вода поступает в неё под достаточно высоким давлением. Выходит же из нее с большой скоростью (см. уравнение неразрывности струи)
 и под низким давлением (согласно правилу Бернулли). Воздух или жидкость откачиваемая трубкой 2 из какой-либо полости отсасывается в
и под низким давлением (согласно правилу Бернулли). Воздух или жидкость откачиваемая трубкой 2 из какой-либо полости отсасывается в
сосуд, а затем через трубку 3 удаляется из него.
Рис. 4.6
Вязкость жидкости.
При течении реальной жидкости между молекулами действуют силы взаимного притяжения, в результате чего возникает внутреннее трение (вязкость).
Ньютон установил, что сила внутреннего трения между
двумя слоями (рис. 4.7) жидкости определятся как 

где  коэффициент внутреннего трения (коэффициент вязкости);
коэффициент внутреннего трения (коэффициент вязкости);  площадь соприкосновения слоёв,
площадь соприкосновения слоёв,
| Рис. 4.7 |  - градиент скорости. - градиент скорости.
|
В векторном виде это уравнение записывается как 
 ,
,
откуда следует, что сила трения ускоряет медленно текущие слои и замедляет быстротекущие слои. Направлена сила трения по касательной к поверхности соприкасающихся слоев.
Смысл градиента скорости легко понять, если считать, что скорости  и
и  какие-то конкретные, постоянные.
какие-то конкретные, постоянные.

 -градиент скорости показывает, на сколько изменяется скорость при изменении направления на единицу меры. Поскольку направление изменения скорости совпадает с толщиной слоя, проще можно сказать, что градиент скорости показывает на сколько изменяется скорость при изменении толщины слоя на единицу.
-градиент скорости показывает, на сколько изменяется скорость при изменении направления на единицу меры. Поскольку направление изменения скорости совпадает с толщиной слоя, проще можно сказать, что градиент скорости показывает на сколько изменяется скорость при изменении толщины слоя на единицу.


Физический смысл коэффициента внутреннего трения определим из формулы (1)

Откуда следует, что коэффициент внутреннего трения показывает, какая сила трения возникает при соприкосновении слоев на площади, равной 1 м2, при градиенте скорости между ними, равном 1 с-1.


Внесистемной единицей является 1 Пуаз; 1 П = 0,1 Па с
У большинства жидкостей коэффициент вязкости зависит только от рода жидкости и от температуры. С повышением температуры коэффициент вязкости уменьшается, т.к. уменьшаются силы взаимодействия между молекулами. Такие жидкости называются ньютоновскими жидкостями.
Ламинарное и турбулентное течение
Свойства течения вязкой жидкости зависят от её плотности  , вязкости
, вязкости  , характерных для данного течения скорости
, характерных для данного течения скорости  и линейного размера
и линейного размера  . При течении жидкости по трубе характерным размером является диаметр трубы, а характерной скоростью - средняя скорость потока.
. При течении жидкости по трубе характерным размером является диаметр трубы, а характерной скоростью - средняя скорость потока.
Характер течения жидкости определяется числом Рейнольдса
 .
.
Рейнольдс определил критическое число  .
.
Если  , то течение является ламинарным, при
, то течение является ламинарным, при  течение является турбулентным.
течение является турбулентным.
Ламинарное течение - это течение, которое носит слоистый характер, слои движутся не перемешиваясь. Оно наблюдается при сравнительно невысоких скоростях. Устанавливается при течении жидкости по трубам с гладкими стенками, без резких изменений площади сечения или изгибов, при отсутствии множественных разветвлений.
При нарушении этих условий течение становится турбулентным.
Турбулентное течение характеризуется вихреобразным движением жидкости, при котором происходит интенсивное перемешивание жидкости в макроскопическом масштабе.
Эти два течения характеризуются различными зависимостями силы сопротивления от скорости. При ламинарном течении
 ~
~  , при турбулентном течении
, при турбулентном течении  ~
~  .
.
Распределение скорости и градиента по сечению
трубы при ламинарном течении.
Рассмотрим течение вязкой жидкости, смачивающей стенки, по горизонтальной трубе постоянного сечения, т.е. ламинарное течение (рис. 4.8). Т.к. жидкость смачивающая, то слой молекул, прилегающих к стенке трубы, прилипает к ней и остается неподвижным. Следующий слой молекул под действием силы давления смещается относительно стенок. Но, т.к. движению молекул противодействуют силы внутреннего трения, скорость смещения этого следующего слоя невелика. Каждый последующий слой, смещаясь относительно предыдущего слоя, движется по отношению к стенке трубы с постоянновозрастающей скоростью. Наибольшее значение скорость имеет в центре трубы.
 Распределение скорости по сечению трубы носит параболический характер:
Распределение скорости по сечению трубы носит параболический характер:
 ,
,
| Рис. 4.8 | где радиус трубы,  радиус рассматриваемого слоя, радиус рассматриваемого слоя,
|
 коэффициент вязкости жидкости,
коэффициент вязкости жидкости,  длина трубы,
длина трубы,  и
и  – давление в начале и конце трубы, соответственно.
– давление в начале и конце трубы, соответственно.
Наибольшее значение скорость имеет в центре трубы:
 ,
,  .
.
Градиент скорости, наоборот максимален в пристеночной части трубы:
 .
.
Течение реальной жидкости
по горизонтальной трубе постоянного сечения.
Закон Гагена-Пуазейля.
При течении жидкости по горизонтальной трубе постоянного сечения (рис. 4.9) потенциальная энергия её частиц расходуется на работу по преодолению внутреннего трения. Поэтому статическое давление вдоль трубы постепенно падает. Для того чтобы обеспечить течение жидкости, необходимо в начале трубы создать давление, превышающее падение давления вдоль всей трубы.

Рис. 4.9
Из рисунка видим, что давление в трубе постоянного сечения понижается равномерно. Если соединить уровни жидкости в манометрических трубках, установленных вдоль трубы, то получится прямая линия. Если её продлить до основного сосуда, то она разделит высоту столба жидкости на две части:  и
и  . Высота
. Высота  соответствует начальному статическому давлению, а высота
соответствует начальному статическому давлению, а высота  – гидродинамическому давлению, обеспечивающему скорость течения жидкости. Крутизна этой кривой (тангенс угла наклона) характеризует продольный градиент давления:
– гидродинамическому давлению, обеспечивающему скорость течения жидкости. Крутизна этой кривой (тангенс угла наклона) характеризует продольный градиент давления:
 .
.  . Градиент давления показывает, на сколько изменяется давление при изменении длины трубы на единицу.
. Градиент давления показывает, на сколько изменяется давление при изменении длины трубы на единицу.
Скорость течения жидкости определяется по формуле (4.11), но ламинарный характер течения определяется средней скоростью.
Пуазейль опытным путем установил, что средняя скорость течения жидкости по горизонтальной трубе постоянного сечения определяется как

 – закон Пуазейля.
– закон Пуазейля.
Количество жидкости, протекающей через поперечное сечение за время Δt,
 .
.
При 
 ,
,  определяется формулой (4.12), а
определяется формулой (4.12), а  .
.
Следовательно,
 закон Гагена-Пуазейля.
закон Гагена-Пуазейля.
Введем величину  и назовем её гидравлическим сопротивлением. Тогда закон Гагена-Пуазейля запишется как
и назовем её гидравлическим сопротивлением. Тогда закон Гагена-Пуазейля запишется как
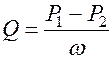 .
.
Гидравлическое сопротивление резко уменьшается при увеличении радиуса трубы, поэтому количество жидкости, протекающее по трубе, увеличивается с увеличением её радиуса.
Течение жидкости по горизонтальной трубе
переменного сечения

Рис. 4.10.
Средняя скорость течения определяется формулой (4.12)
 ,
,
т.е.  . Поэтому на участках трубы различного сечения скорости различны (манометрические трубки установлены в начале и конце каждого участка). Соответственно изменяются и градиенты давлений. К тому же по правилу Бернулли статическое давление невязкой жидкости при течении по горизонтальной трубе увеличивается там, где скорость её уменьшается, и наоборот. Кроме того, в местах изменения сечения трубы течение становится турбулентным, что вызывает потери энергии. Кроме того, из закона Гагена – Пуазейля,
. Поэтому на участках трубы различного сечения скорости различны (манометрические трубки установлены в начале и конце каждого участка). Соответственно изменяются и градиенты давлений. К тому же по правилу Бернулли статическое давление невязкой жидкости при течении по горизонтальной трубе увеличивается там, где скорость её уменьшается, и наоборот. Кроме того, в местах изменения сечения трубы течение становится турбулентным, что вызывает потери энергии. Кроме того, из закона Гагена – Пуазейля,  следует, что, поскольку количество жидкости, протекающее через поперечное сечение, не меняется, то меняется градиент давлений: при переходе от меньшего сечения к большему давление падает меньше, а при переходе от большего сечения к меньшему давление падает больше.
следует, что, поскольку количество жидкости, протекающее через поперечное сечение, не меняется, то меняется градиент давлений: при переходе от меньшего сечения к большему давление падает меньше, а при переходе от большего сечения к меньшему давление падает больше.
Течение жидкости по разветвленной трубе

Рис. 4.11
В разветвленной трубе градиент давлений зависит:
1) от общего сечения разветвленной части, т.к. от этого зависит средняя скорость течения жидкости, и, следовательно, общие потери энергии.
2) От числа труб в разветвленной части. Это легко понять, если вспомнить формулу Ньютона  . Сила трения зависит от градиента скорости, который имеет наибольшее значение около стенок трубы. Поэтому потери энергии на преодоление силы трения в пристеночном слое выше, чем в центральной части. А поскольку в разветвлении площадь пристеночного слоя велика, то и потери энергии большие.
. Сила трения зависит от градиента скорости, который имеет наибольшее значение около стенок трубы. Поэтому потери энергии на преодоление силы трения в пристеночном слое выше, чем в центральной части. А поскольку в разветвлении площадь пристеночного слоя велика, то и потери энергии большие.
Чем больше трубок, тем больше потери энергии, тем больше падает давление.
Течение жидкости по эластичной трубе
Если жидкость течет по эластичной трубе, то упругие свойства материала стенок влияют на характер течения жидкости. При поступлении жидкости в трубу труба растягивается, а затем, сжимаясь, проталкивает жидкость силой обратной деформации.
Лекция 5.
Биореология.
Биореология - раздел физики, изучающий течение биоло-гических жидкостей, обладающих вязкостью и пластичных.
В предыдущей лекции мы отметили, что у большинства жидкостей коэффициент вязкости зависит от природы жидкости и от температуры. Эти жидкости называются ньютоновскими жидкостями.
У некоторых жидкостей, преимущественно высокомолекулярных, коэффициент вязкости зависит не только от температуры и природы жидкости, но и от режима течения, градиента скорости, давления и др. факторов. Такие жидкости называются неньютоновскими. В качестве примера неньютоновских жидкостей кровь. Это пластичная, вязкая жидкость. Она относится к неньютоновским жидкостям из-за своего состава: кровь – это суспензия форменных элементов в белковом растворе- плазме.
В биореологии из-за пластичности жидкостей формула Ньютона  записывается в иной форме
записывается в иной форме
 .
.
Это связано с тем, что высокомолекулярные вещества образуют крупные агрегаты и их следует рассматривать как сплошные среды. Например, кровь образует агрегаты в виде монетных столбиков из эритроцитов. В расчет принимаются только
эритроциты, т.к. 
эритроцитов в крови  в 50 раз больше, чем тромбоцитов и лейкоцитов. Поэтому реологические свойства кро-
в 50 раз больше, чем тромбоцитов и лейкоцитов. Поэтому реологические свойства кро-
| Рис. 5.1 | ви определяются толь-ко концентрацией и. |
механическими свойствами эритроцитов. Как видно из рисунка при движении крови наблюдается деформация сдвига. Поэтому формулу Ньютона преобразуют в формулу, похожую на закон Гука, описывающий деформацию твердых тел.
В уравнении (5.1)  - напряжение сдвига,
- напряжение сдвига,  - скорость сдвига.
- скорость сдвига.
Дата добавления: 2016-01-20; просмотров: 847;
