Классификация медицинской электронной аппаратуры 2 страница

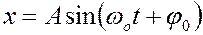, то , то 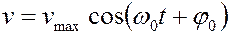потенциальная энергия определиться как

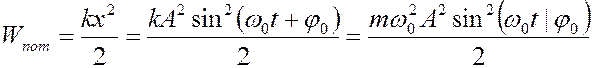
т.к. 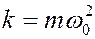, а кинетическая энергия определиться как

.

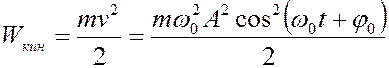Полная энергия, таким образом, определяется как

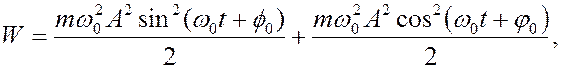откуда

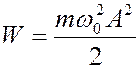
Затухающие колебания

Реальные механические колебания, т.е. колебания, происхо-дящие в природе, совершаются в среде. Значит, на колеблющуюся точку кроме возвращающей силы действует еще сила трения:

,

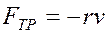где 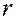– коэффициент трения. Следовательно, реальные колебания являются затухающими, т.к. энергия колеблющейся точки теряется на преодоление силы трения.

Теперь уравнение движения колеблющейся точки следует записать в виде

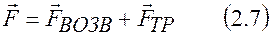
или в скалярном виде в проекциях на ось ОХ

.

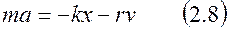Заменяя 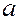и 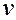через производные, получим

.

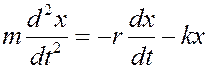
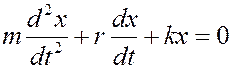Деля на 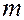обе части уравнения и вводя обозначения 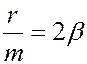( - коэффициент затухания) и 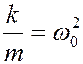, получим дифференциальное уравнение второго порядка для затухающих колебаний

.

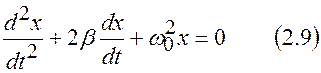Решением этого уравнения является функция

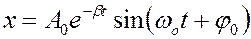или

.

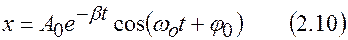Здесь 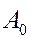– амплитуда первого колебания.

Анализируя решение, следует отметить, что амплитуда затухающих колебаний с течением времени уменьшается с течением времени по экспоненциальному закону из-за потерь энергии точки на преодоление силы трения и определяется в любой момент времени как

.

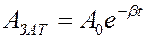Само же колебание остается гармоническим и происходит с периодом 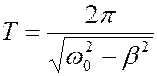. График зависимости смещения затухающего колебания от времени приведен на рис. 2.5.

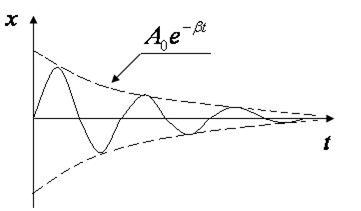
Рис. 2.5

Быстроту затухания, т.е. быстроту убывания амплитуды, определяют логарифмическим декрементом затухания

или, после подстановки в это отношение значений амплитуд в моменты времен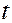и и ,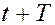

.

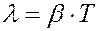Вынужденные колебания

Чтобы компенсировать потери энергии на преодоление силы трения, необходимо колеблющейся точке извне добавлять энергию, т.е. необходимо действовать на точку внешней вынуж-дающей силой 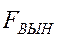_. Эта сила должна удовлетворять следующим требованиям: она должна быть периодической и иметь частоту 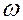, отличную от частоты собственных колебаний точки, 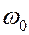, т.е. её можно записать как

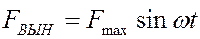
где - амплитуда вынуждающей силы.

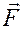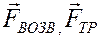Следовательно, при вынужденных колебаниях точка движется под действием равнодействующей сил и 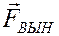. Уравнение движения теперь запишется в виде

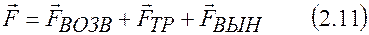
или в проекциях на ось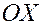

.

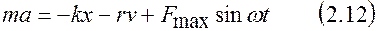После деления на m и введения применяемых ранее обозначений, получим дифференциальное уравнение 2-го порядка для вынужденных колебаний

.

Решением этого уравнения является функция

.

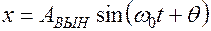Точнее

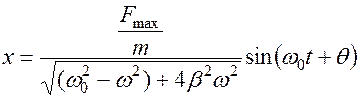
Здесь – амплитуда вынужденных колебаний. Как видим, она зависит от частоты и амплитуды вынуждающей силы. Анализируя решение, замечаем, что колебания точки происходят с частотой вынуждающей силы, колебание остается гармоническим с новой начальной фазой .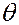

Если коэффициент затухания стремится к нулю (это возможно при малом сопротивлении), то

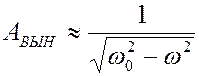
График смещения вынужденных колебаний показан на рис.2.6. Начальный период мы не рассматриваем. Все проведенные выше рассуждения касались только установившихся вынужденных колебаний.

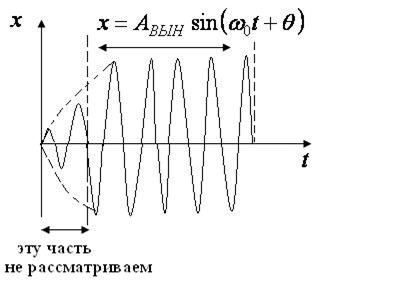
График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы при различных коэффициентах затухания показан на рис.2.7.

Рис. 2.6

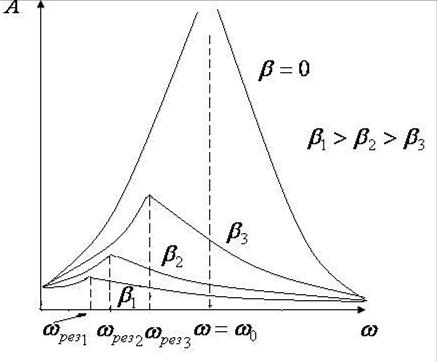
Рис.2.7

При выполнении условия амплитуда 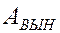резко возрастает 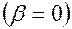. Это явление резкого возрастания амплитуды при равенстве собственной частоты колебаний точки и частоты вынуждающей силы называется явлением механического резонанса.

Явление механического резонанса может быть полезным: при малых усилиях можно увеличить амплитуду колебания; но может быть и вредным: разрушение, действие вибраций на организм. Предупреждают резозанс тем, что создают колебания с частотой 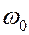, отличной от частоты 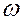вынуждающей силы.

Автоколебания

Мы выяснили, что амплитуда вынужденных колебаний зависит от амплитуды 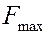и частоты внешней, вынуждающей, силы.

Это означает, что внешнее воздействие “управляет” колебаниями системы и сообщает ей энергию, не согласовываясь с процессами, происходящими в системе. Можно создать такую систему, в которой вынужденные колебания происходят с собственной частотой. Такие системы называются автоколебательными, а происходящие в них колебания - автоколебаниями.

Механическая автоколебательная система содержит источник внешней силы, постоянной по величине и направлению, которая периодически в необходимые моменты “подталкивает” колеблющееся тело и таким образом поддерживает его свободные колебания незатухающими. Блок-схема автоколебательной системы представлена на рис. 2.8.

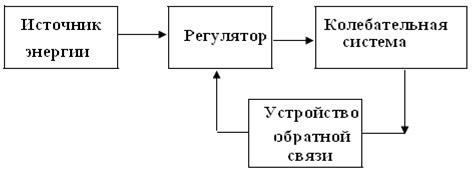
Рис. 2.8.

Сложение колебаний

Колебательное движение, при котором смещение описывается во времени любым законом, но не законом синуса или косинуса, является сложным колебанием. Сложное колебание – это результат сложения простых, гармонических, колебаний. Поэтому мы должны уметь складывать колебания.

Смещение тела, участвующего одновременно в двух или нескольких колебаниях, находится на основании принципа суперпозиции, согласно которому эти колебания накладываются, не влияя одно на другое.

I.Однонаправленные колебания.

Пусть материальная точка одновременно участвует в двух колебаниях, происходящих вдоль одной линии. Смещения этой точки для каждого колебания описывается уравнениями

,

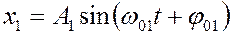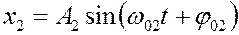
а) Если 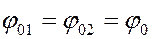; 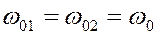, но 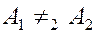_то смещение результирующего колебания описывается как

.

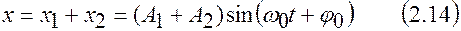б) В общем случае при условии, что ,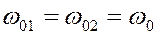

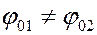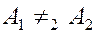, , сложение удобнее проводить с использованием метода векторных диаграмм.

При указанных условиях смещения точки запишутся как

,

,

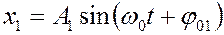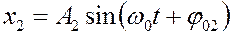а смещение результирующего колебания определится как

.

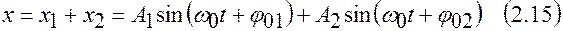Смещение результирующего колебания будем описывать уравнением

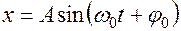
Для расчета амплитуды результирующего колебания построим векторную диаграмму. Из точки 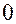системы координат ХОУ (рис.2.9) проведем векторы 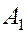и 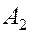под углам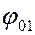и и 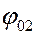к оси ОХ, соответственно. Длины этих векторов равны модулям амплитуд 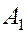и 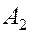складывающихся колебаний. Векторы 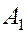и 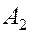вращаются с одинаковой частотой, следовательно, вектор будет вращаться с той же частотой.

Амплитуду результирующего колебания найдем из треугольника 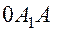, применив теорему косинусов

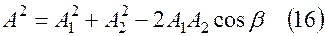Т.к. ,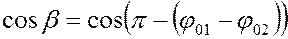

то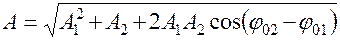

рис. 2.9

Начальная фаза 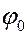результирующего колебания находится как

= = .

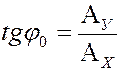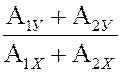Частные случаи:

1) , ,

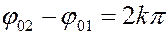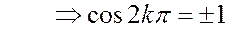где

Тогда 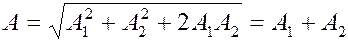- усиление колебаний (рис.2.10):

Рис. 2.10

2) ,

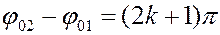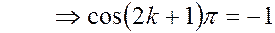
Тогда 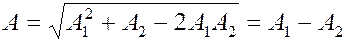- ослабление колебаний (рис.2.11):

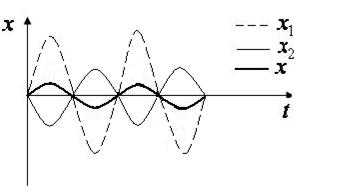
Рис. 2.11

Биения. Если частоты слагаемых колебаний мало отли-чаются, т.е. , то результирующее колебание будет подобно гармоническому колебанию с медленно изменяющейся амплитудой. Наблюдается амплитудная модуляция. Такие колебания называются биениями (рис. 2.12)

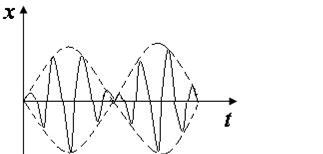
Рис. 2.12

2. Взаимноперпендикулярные колебания.

Возможна ситуация, при которой точка участвует одновременно в двух взаимноперпендикулярных колебаниях: одно направлено вдоль оси ОХ, другое - вдоль оси ОУ. Смещения точек описываются при этом уравнениями (считаем, что собственная частота 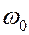у обоих колебаний одинакова):

,

.

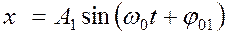Исключая из этих уравнений время t, получим уравнение

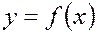в виде

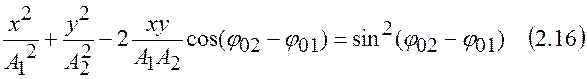
Это и есть уравнение траектории, по которой движется точка, а именно, уравнение эллипса (рис.2.13).

Рис. 2.13

Конкретный вид траектории зависит от разности фаз 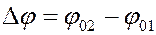. Если 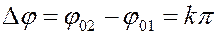, где ,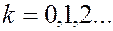

то 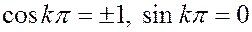, и уравнение (2.16) запишется как

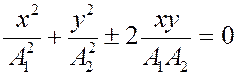
или после преобразований

, , ,

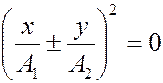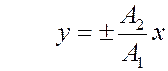т.е. получаем уравнения прямой, по которой будет двигаться точка (рис.2.11 соответствует знаку 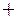, рис.2.12 соответствует знаку -).

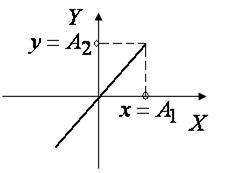
Рис.2.11	Рис.2.12

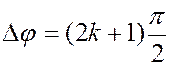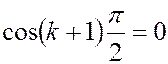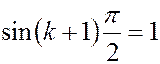Если , то , , и уравнение (2.16) запишется как

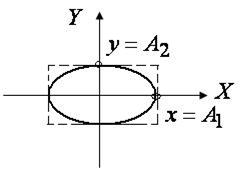
Это уравнение эллипса, расположенного симметрично относительно осей координат. Именно такую траекторию будет описывать точка (рис. 2.13).

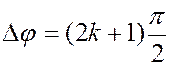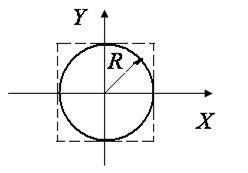
Если при такой разности фаз, , амплитуды равны между собой ( 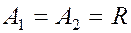), то уравнение (2.17) станет уравнением окружности (рис. 2.14).

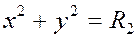
Рис. 2.13	Рис. 2.14

Траектории, по которым движется точка в результате сложения колебаний, называются фигурами Лиссажу.

Сложное колебание. Гармонический спектр сложного колебания.

В природе наблюдаются сложные колебания – колебательное движение, при котором смещение точки описывается не по гармоническому закону, а по любому другому периодическому закону

На практике очень часто такие сложные колебания приходится раскладывать на простые, т.е. решать задачу, обратную сложению колебаний. Вопрос разложения сложных колебаний на простые решил Фурье, поэтому при разложении сложного колебания на простые мы пользуемся теоремой Фурье: “Любое сложное периодическое колебание может быть представлено суммой простых гармонических колебаний, периоды или частоты которых кратны периоду или частоте основного колебания”.

Совокупность простых колебаний, на которые раскладывается сложное колебание, называется гармоническим спектром сложного колебания.

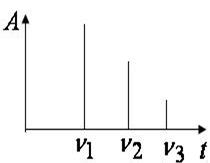
Пример: на рис. 2.15 представлен график сложного колебания (сплошная линия) и простых колебаний (пунктир) с частотами n₁, n₂, n₃, на которые оно может быть разложено, а на рисунке 2.16 – гармонический спектр этого сложного колебания.

Рис. 2.15	Рис. 2.16

Гармонический спектр позволяет провести анализ сложного колебания. Очевидно, каждая гармоника описывает какой-то отдельный процесс, вносящий свой вклад в общее колебание.

В лабораториях, в том числе и медицинских, разложение колебаний и анализ их производится автоматически с помощью приборов, называемых анализаторами или Фурье-спектро-метрами

Механические волны.

Если же рассматривать колебания точки в среде, где она взаимосвязана с другими точками, то колебания данной точки среды будет передаваться другой точке, затем к третьей и т.д. Процесс распространения колебаний в данной упругой среде, при котором происходит процесс переноса энергии без переноса вещества, называется волновым процессом.

В результате внешнего воздействия на среде в ней возникает возмущение – отклонение частиц среды от положения равновесия. Механическая волна – возмущение, распространяющееся в упругой среде.

Рассмотрим образование поперечных волн (рис.2.16). Поперечная волна – это волна, в которой частицы среды перемещаются перпендикулярно направлению распространения волны.

Точка 1 приводится в гармоническое колебание с периодом Т, так что она движется перпендикулярно линии 1-8. Через время

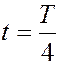точка .1 сместится максимально относительно положения равновесия и передаст свою энергию точке 2.В момент времени

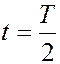точка 1 возвращается в положение равновесия, точка 2 отклонится максимально, точка 3 начинает колебаться. Последовательно в процесс включаются все частицы среды.

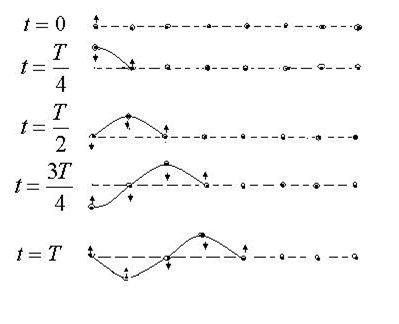
В среде образуется волна, в которой каждая частица движется только вверх и вниз. Наблюдатель видит бегущие частицы, а на самом деле происходит только передача энергии от одной частицы к другой.

твердых телах, в которых имеются внутренние упругие силы, противодействующие деформации сдвига. Поперечные волны не могут возникать в газах и жидкостях, т.к. в них отсутствует фиксированное положение частиц и, следовательно, противодействие деформации сдвига, но на свободной поверхности жидкости под действием сил тяжести и поверхностного натяжения, стремящихся поддержать горизонтальный уровень поверхности, поперечные волны возникают.

Продольная волна – это волна, в которой колебания частиц среды происходят в направлении распространения волны. Продольные волны могут распространяться в средах, имеющих внутренние силы, противодействующие деформации объёмного сжатия, т.е. во всех средах.

Образование продольной волны показано на рис. 2.17.

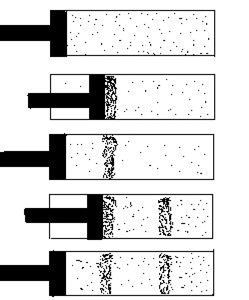В стеклянный цилиндр с воздухом

вставлен с одного конца поршень,

который совершает гармоническое

колебание вдоль оси цилиндра.

Движение поршня вызывает

колебания в том же направалении

прилегающих к нему частиц возду-

ха и образование в нем участков сгущения, а затем на тех же участках разряжения частиц. Т.к. воздух – упругая среда, колебания передаются соседним частицам, возникают новые участки сгущения и разряжения

Основной характеристикой волны является длина волны l -

это расстояние между двумя ближайшими точками волны, колеблющимися в одной фазе, что соответствует периоду Т колебания. Иначе можно сказать, что длина волны – это расстояние, на которое волна распространяется за время одного периода

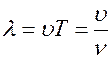, т.к.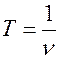

Здесь u - скорость распространения волны – скорость, с которой перемещается в среде любая фиксированная фаза волны, например, гребни волны.

Уравнение плоской механической волны.

В однородной изотропной среде колебания, возбуждаемые в одной точке, распространяются от неё равномерно по всем направлениям; такая волна называется сферической. Если источник колебаний имеет значительную плоскую поверхность, то волна от него распространяется параллельным потоком, направленным перпендикулярно поверхности источника. Такая волна называется плоской. Уравнение плоской волны выражает зависимость смещения любой колеблющейся точки, участвующей в волновом процессе, от координаты её равновесного положения и времени, 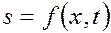. Выведем это уравнение, считая, что волна распространяется вдоль оси ОХ, без затухания так, что амплитуды колебаний всех точек среды одинаковы для всех точек среды:

Пусть в точке находится точка В среды, которая первая начинает колебания, вибратор, так что смещение её описывается уравнением

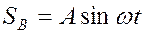
До точки среды С, находящейся на расстоянии от точки В, возмущение дойдет с некоторым запозданием на время 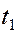, так что время колебаний точки С будет определяться как 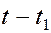, а смещение её опишется уравнением

.

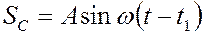Время запаздывания можно определить как , где – скорость распространения волны. Уравнение смещения точки С запишется теперь как

.

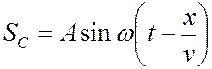Такое же уравнение мы можем записать для любой точки среды. Поэтому мы можем сказать, что уравнение плоской волны есть:

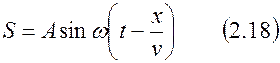
Т.к. 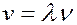и , то уравнение (2.18) можно записать как

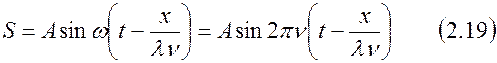
Для любого конкретного времени, 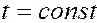, уравнение волны представляет зависимость смещения только от расстояния 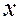: 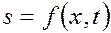. График зависимости 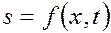представляет собой как бы фотографию волны в момент времени 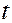. Для гармонической волны график показан на рисунке 2.18.

Рис. 2.18.

Если график волны, приведенный на рис.2.18, отнести к некоторому времени 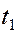, то для других моментов времени 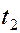, 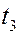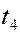_, график перемещается вдоль оси 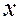со скоростью u распространения волны. Кривые, соответствующие указанным моментам времени, показаны штриховыми линиями.