Дисконтирование по простым процентным ставкам. Наращение по учетной ставке
В финансовой практике часто сталкиваются с задачей, обратной наращению процентов: по заданной сумме FV, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды PV. В этом случае говорят, что сумма FV дисконтируется или учитывается, сам процесс начисления процентов и их удержание называют учетом, а удержанные проценты – дисконтом или скидкой. Необходимость дисконтирования возникает, например, при покупке краткосрочных обязательств, оплата которых должником произойдет в будущем момент времени.
В более широком смысле дисконтирование – это средство приведения любой стоимостной величины, относящейся к будущему, на более ранний момент времени.
Величину PV, найденную с помощью дисконтирования, называют современной стоимостью, или современной величиной будущего платежа FV, а иногда текущей, или капитализированной, стоимостью.
В зависимости от вида процентной ставки применяют два метода дисконтирования – математическое дисконтирование и банковский (коммерческий) учет. В первом случае применяется ставка наращения, во втором – учетная ставка.
1. Математическое дисконтированиепредставляет собой формальное решение задачи, обратной наращению первоначальной суммы ссуды. Задача в этом случае формулируется так: какую первоначальную сумму ссуды надо дать в долг, чтобы получить в конце срока сумму FV, при условии, что на долг начисляются проценты по ставке i.
Формула математического дисконтирования по простой процентной ставке имеет вид:
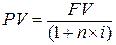 .
.
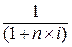 - дисконтный множитель.
- дисконтный множитель.
Пример: Через 180 дней после подписания договора должник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дням?
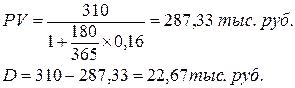
Разность D можно рассматривать не только как проценты, начисленные на PV, но и как дисконт с суммы FV.
2. Банковский учет (учет векселей). Суть операции заключается в следующем: банк или другое финансовое учреждение до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.е. покупает (учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует процентный доход в виде дисконта. В свою очередь владелец векселя с помощью его учета имеет возможность получить деньги хотя и не в полном объеме, однако раньше указанно на нем срока.
При учете векселя применяется банковский, или коммерческий, учет. Согласно этому методу проценты за пользование ссудой в виде дисконта начисляются на сумму, подлежащую уплате в конце срока. При этом применяется учетная ставка d.
Формула банковского учета по простой учетной ставке имеет вид:
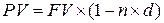 ,
,
где n – срок от момента учета до даты погашения векселя.
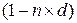 - дисконтный множитель.
- дисконтный множитель.
Учет посредством учетной ставки чаще всего осуществляется при временной базе k = 360 дней, число дней ссуды обычно берется точным (365/360).
Пример: Вексель выписан на сумму 100 тыс. руб. с уплатой 17 ноября 2012 г. Владелец векселя учел его в банке 23 сентября 2012 г. по простой учетной ставке 20% годовых. Определить полученную при учете сумму и дисконт.
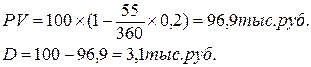
Операции начисления процентов и дисконтирования по учетной ставке могут совмещаться. Например, при учете долгового обязательства, предусматривающего начисление простых процентов, следует решить две задачи:
1. Определение наращенной стоимости (FV).
2. Расчет суммы, полученной при учете (PV).
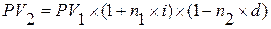 ,
,
где 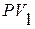 - первоначальная сумма ссуды;
- первоначальная сумма ссуды;
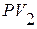 - сумма, полученная при учете;
- сумма, полученная при учете;
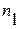 - общий срок платежного обязательства (срок начисления процентов);
- общий срок платежного обязательства (срок начисления процентов);
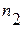 - срок от момента учета до даты погашения долгового обязательства, причем
- срок от момента учета до даты погашения долгового обязательства, причем 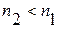 .
.
Пример: Дополним условия предыдущего примера. Пусть на первоначальную сумму (100 тыс. руб.) теперь начисляются простые проценты по ставке 20,5 % годовых. Определить наращенную сумму долга и сумму, полученную при учете, если общий срок платежного обязательства – 120 дней.
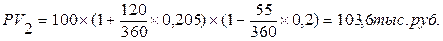
Наращение по учетной ставке
Простая учетная ставка иногда применяется и при расчете наращенной суммы. В частности, в этом возникает необходимость при определении суммы, которую надо проставить в векселе, если задана текущая сумма долга. Наращенная сумма в этом случае
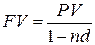 .
.
Множитель наращения здесь равен 1/(1-nd).
Дата добавления: 2016-01-20; просмотров: 6720;
