Ток короткого замыкания в произвольный момент времени

Действующее значение периодической составляющей тока основной частоты в любой момент времени в период от начала короткого замыкания до наступления установившегося режима определяется выражением

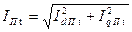, (4.8)

где 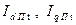- произвольные значения периодических составляющих по осям d и q синхронной машины.

Из [2]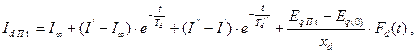

,

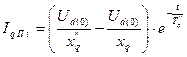где 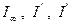- соответственно периодические составляющие установившегося, переходного и сверхпереходного токов КЗ.

Постоянные времени затухания токов определяются выражениями

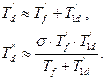
Постоянная времени обмотки возбуждения при замкнутой статорной и разомкнутой демпферной обмотках:

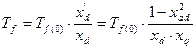
Значения параметров, входящих в выражение для определения постоянных времени, рассчитываются по формулам:

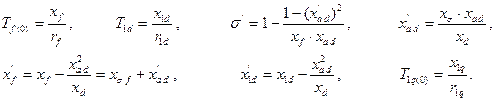
Функция ),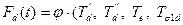

где 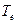– постоянная времени системы возбуждения, .

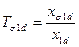Полный ток короткого замыкания фаз в произвольный момент времени состоит из периодической составляющей, апериодической составляющей и составляющей двойной частоты, обусловленной несимметрией ротора и наличием апериодической составляющей тока статора [9].

Например, ток фазы А:

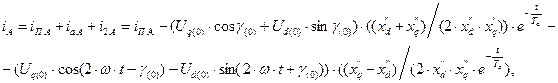(4.8)

где 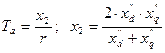– сопротивление обратной последовательности.

Выражение (4.8) показывает, что точный расчет токов короткого замыкания в произвольный момент времени в сложных СЭС, содержащих, кроме источников питания, мощные нагрузки, весьма затруднителен.

Учитывая это обстоятельство, а также отсутствие точных данных и разнообразие возможных режимов работы СЭС, для вычисления токов КЗ в произвольный момент времени, практически используют приближенные методы расчета.