Неразветвленные и разветвленные магнитные цепи

Задачей расчета неразветвленной магнитной цепи чаще всего является определение МДС F = I∙w (3.4), необходимой для вычисления тока в катушке I, магнитного потока Ф или магнитной индукции В в некотором сечении S_К магнитопровода.

Учитывая, что магнитный поток во всей неразветвленной цепи одинаков, значение магнитной индукции в к-ом сечении

В_К = Ф / S_К = μ_аК Н_К. (3.6)

Из (3.6), с учетом (10.5) получим:

Н_К = В_К / μ_а и далее 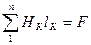. (3.7)

Рассмотрим схему магнитной цепи, состоящую из магнитопровода с катушкой (Рис. 3.4), для которой магнитный поток Ф известен. Требуется определить величину тока I в катушке с количеством витков w, необходимую для создания требуемого магнитного потока. Цепь состоит из двух участков, геометрические параметры которых l₁, S₁ и l₂ , S₂ (l - длина участка, S – поперечное сечение участка). Магнитные свойства материала заданы зависимостью В = μ_а Н.

Если магнитный поток Ф задан, то он будет одинаковым для любого сечения магнитопровода

Ф = В₁ S₁ = В₂ S₂ .

Тогда согласно формуле (3.7)

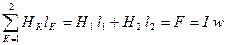, (3.8)

где Н₁ и Н₂ напряженности магнитного поля в первом и втором участках магнитопровода.

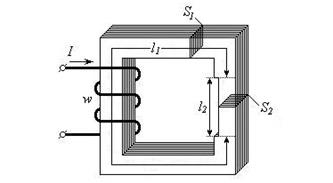
Рис. 3.4 – Простая магнитная цепь

Согласно закону Ома (3.5) для заданной магнитной цепи

Ф = F /( r_{M 1} + r_{M 2}). Тогда, с учетом (3.8), получим искомый ток

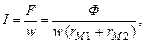(3.9)

где r_M1 = l₁ / S₁ μ_а - магнитное сопротивление участка длиной l₁;

r_{M 2} = l₂ / S₂ μ_а - магнитное сопротивление участка длиной l₂.

В этих соотношениях μ_а = μ_а (Н), то есть является нелинейной величиной.

Обратная задача, когда требуется при известной МДС F определить магнитный поток Ф, сложнее. Решение можно получить графическим путем, используя магнитную характеристику цепи F = f(Ф).

В разветвленной магнитной цепи (например, изображенной на рис. 3.1, б) могут существовать несколько магнитных потоков, которые на определенных участках могут складываться или вычитаться. Здесь используются аналогии с первым и вторым законами Кирхгофа.

Первый закон Кирхгофа для магнитной цепи гласит: в любом узле разветвленной магнитной цепи алгебраическая сумма магнитных потоков равна нулю:

(3.10)

Второй закон Кирхгофа для магнитной цепи формулируется так: в любом контуре магнитной цепи алгебраическая сумма магнитодвижущих сил равна алгебраической сумме призведений магнитных потоков в ветвях данного контура и магнитных сопротивлений этих ветвей:

(3.11)