Схема замещения однофазного трансформатора

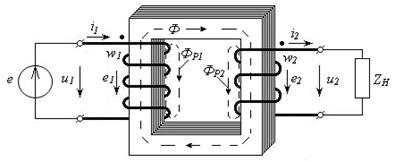
Рассмотрим однофазный трансформатор, схема устройства которого приведена на рис.3.10. К первичной обмотке трансформатора, содержащей w₁ витков, подключен идеальный источник переменной ЭДС е = Е_т sin ωt. Нагрузка Z_H подсоединена к вторичной обмотке, имеющей w₂ витков.

Рис.3.10 – Однофазный трансформатор

Здесь следует заметить, что при показанных на рисунке направлениях намотки катушек и направлениях токов i₁ и i₂ магнитные потоки этих катушек будут направлены встречно (убедиться можно, используя правило буравчика). Если бы ток i₂ имел обратное направление по отношению к зажиму второй катушки, помеченному жирной точкой (как в первой катушке), то магнитные потоки катушек сложились бы. Помеченные зажимы называют одноименными.

За счет тока i₁ на входе трансформатора создается падение напряжения u₁ и формируется магнитный поток Ф, общий для первой и второй катушек, и возникает магнитный поток рассеяния Ф_Р1. Так как ЭДС е переменная, то ток i₁ и магнитный поток Ф также будут переменными. За счет изменения магнитного потока Ф в обмотках трансформатора будут создаваться ЭДС (самоиндукции е₁ и взаимной индукции е₂)

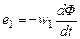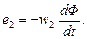и (3.20)

Положительные направления ЭДС е₁ и тока i₁ в первичной катушке совпадают. Знак «минус» в выражениях (3.20) физически объясняется тем, что в первой катушке ЭДС препятствует изменению тока i₁, а во второй возбуждает ток i₂. За счет тока i₂ во вторичной катушке будет формироваться магнитный поток рассеяния Ф_Р2 и на нагрузке Z_H – напряжение u₂.

Для перехода к схеме замещения необходимо учитывать, что катушки обладают активными сопротивлениями R₁ и R₂ и индуктивными сопротивлениями рассеяния jX_P1 и jX_P2. Потери на гистерезис и индуктивность, связанную с общим для обеих катушек магнитным потоком Ф, можно учесть с помощью идеализированной катушки, обладающей активным сопротивлением R_Г ииндуктивным сопротивлением jωL₀. Представить трансформатор как участок цепи, имеющий два входных и два выходных зажима позволяет Т-образная схема замещения (Рис. 3.11).

Комплексный коэффициент передачи трансформатора по напряжению от входа к выходу

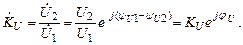(3.21)

Учитывая, что для ненагруженного трансформатора входное напряжение 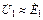a выходное напряжение 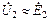, то коэффициент 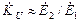. На основании (3.21) и без учета фаз получим, что коэффициент передачи по напряжению трансформатора

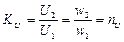(3.22)

Можно также показать, что для токов I₁/I₂≈n_I.

Величину n_U или просто n = U₂/U₁=w₂ /w₁ называют коэффициентом трансформации по напряжению. Соотношение (3.22) справедливо только для ненагруженного трансформатора.

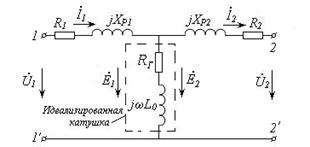
Рис.3.11 – Схема замещения однофазного трансформатора

Если трансформатор имеет несколько вторичных обмоток, то соотношение (3.22) будет применимым для каждой из них. Например, у силового трансформатора, рассчитанного на напряжение сети U₁=220В число витков первичной обмотки w₁ = 330. Трансформатор содержит две вторичные обмотки с количеством витков w₂=36 и w₃=18. Для данного трансформатора первый коэффициент трансформации примерно равен 0,11 и второй 0,055. Выходные напряжения: U_ВЫХ1= 0,11∙220 ≈ 24В; U_ВЫХ2= 0,055∙220 ≈ 12В.

Можно также соединив последовательно выходные обмотки получить и третье напряжение U_ВЫХ3= U_ВЫХ1 + U_ВЫХ2 = 24 + 12 = 36В. Однако здесь необходимо обеспечить согласное включение этих обмоток. При встречном включении получим разность выходных напряжений, что используется редко.