Катушка индуктивности в цепи переменного тока

В цепях переменного тока часто используются катушки индуктивности с сердечниками и с магнитопроводами из ферромагнитных материалов. При расчете электрических цепей, содержащих такие элементы, возникает потребность в схемах их замещения, позволяющих упростить расчет.

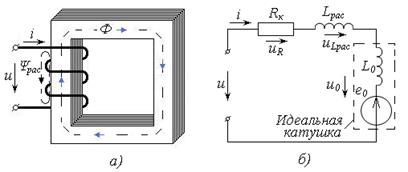
Рассмотрим катушку индуктивности с магнитопроводом, имеющую w витков провода с сопротивлением R_к (Рис. 3.5, а). За счет тока i катушки в магнитопроводе будет формироваться магнитный поток Ф – как основной, и магнитный поток рассеяния, характеризуемый потокосцеплением Ψ_рас .

Потокосцепление рассеяния Ψ_рас зависит от конструкции катушки и, практически, не зависит от магнитопровода. Магнитные силовые линии потока рассеяния замыкаются, в основном, по воздуху и только частично проходят по магнитопроводу.

В воздухе магнитная индукция В = μ₀ Н, где μ₀ - постоянная величина. Поэтому можно считать, что потокосцепление и ток будут связаны линейной зависимостью:

Ψ_рас = L_расi , (3.12)

где L_рас – индуктивность рассеяния обмотки.

Рис. 3.5 –Катушка индуктивности в цепи переменного тока: а) катушка индуктивности с магнитопроводом; б) схема замещения катушки с магнитопроводом

Потокосцепление основного магнитного потока равно wФ. Тогда полное потокосцепление для рассматриваемой катушки

Ψ = w Ф + Ψ_рас . (3.13)

С учетом активного сопротивления катушки R_к и потоко-сцепления Ψ (3.13) напряжение u на зажимах катушки

u = R_к i + = 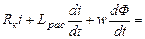u_R + u_Lpac + u₀. (3.14)

Из (3.14) следует, что катушку с ферромагнитным сердечником можно представить в виде последовательно соединенных активного сопротивления R_к, индуктивного элемента L_рас и идеальной катушки индуктивности с индуктивностью L₀ , которая не имеет индуктивности рассеяния (Рис. 3.5, б). Физически идеальную катушку индуктивности можно представить в виде катушки с ферромагнитным сердечником, заключенной в ферромагнитный экран, за пределы которого магнитное поле не проникает.

Для идеальной катушки индуктивности

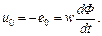(3.15)

Получим для идеальной катушки индуктивности закон изменения магнитного потока Ф. Пусть напряжение u₀. = U_0m sin ωt . Подставив u₀ в (3.15), получим:

dФ = 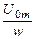sin ωt dt. (3.16)

Проинтегрировав (3.16), получим:

Ф = 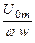sin (ωt + π/2) + А.

Для переменного тока постоянная интегрирования А = 0. Тогда

Ф = sin (ωt + π/2), (3.17)

где U₀ – действующее значение напряжения u₀ .

Амплитудное значение магнитного потока

Ф_m 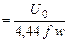. (3.18)

В выражении (3.18) f – циклическая частота. Сомножитель в знаменателе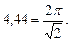

Если задан магнитный поток Ф, то действующее значение напряжения u₀ можно найти как

U₀ = Е₀ = 4,44 f w Ф_т . (3.18)

Выражение (3.18) удобно для расчета ЭДС, индуктируемых в обмотках трансформаторов и других электрических машин.

Схема замещения катушки индуктивности с магнитопроводом в цепи переменного тока, приведенная на рис. 3.2, б, не учитывает потерь энергии магнитного поля на гистерезис (перемагничивание) материала магнитопровода.

Если воспользоваться законом Ома в комплесной форме и определить комплексное сопротивление идеализированной катушки, то получим:

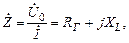(3.19)

где R_Г – активное сопротивление, учитывающее потери электрической энергии на гистерезис; X_L = jωL₀ – индуктивное сопротивлениеидеализированной катушки (Рис.3.6).

Рис.3.6 – Схема замещения катушки индуктивности с магнитопроводом