Временные характеристики

Для исследования динамических свойств систем автоматического управления часто используются типовые переходные режимы работы (временные характеристики). Наибольшее применение находят следующие временные характеристики:

· переходная функция (характеристика) – реакция системы на единичный скачкообразный сигнал при нулевых начальных условиях;

· весовая функция (импульсная переходная характеристика) – реакция непрерывной системы на воздействие в виде δ-импульса Дирака, а для дискретной системы – на единичный импульс.

· реакция системы на ненулевые начальные условия.

По временным характеристикам можно определить ряд качественных показателей, характеризующих динамические свойства системы управления, в частности, перерегулирование, время переходного процесса и др.

В пакете Control System Toolbox имеется ряд функций для расчета и построения временных характеристик линейных систем. Основными из них являются step, impulse, initial.

Функция step вычисляет и отображает на экране переходную характеристику lti-модели. Она имеет несколько форм:

step (sys)

step (sys,t)

step (sys1, sys2,… ,sysN)

step (sys1, sys2,… ,sysN, t)

step (sys1, 'plotstyle1',… ,sysN, 'plotstyleN')

step (sys1, 'plotstyle1',… ,sysN, 'plotstyleN', t).

Здесь t – аргумент, задающий время моделирования в виде длительности переходного режима t=Tfinal (в секундах) или в виде вектора t=0:dt:Tfinal. Для дискретных моделей dt=T_s, а для непрерывных выбирается достаточно малым для учета быстрых изменений переходного процесса. Продолжительность моделирования при отсутствии аргумента t определяется автоматически. Остальные параметры функции step такие же, как в функциях nyquist и bode.

Пример 2.15.Построение переходной характеристики для непрерывной САУ с ПФ Ф(s) (рис.2.6).

>> step(f); grid on

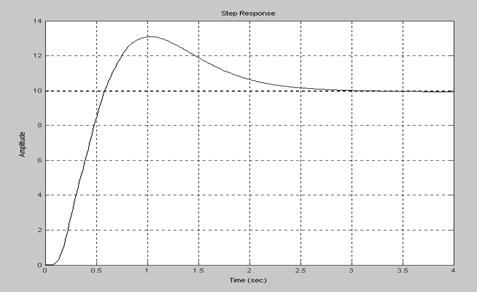
Рис. 2.6. Переходная характеристика

Задание 2.15.Постройте переходную функцию для дискретной САУ, заданной передаточной функцией замкнутой системы Т(z).

Для расчета переходной характеристики без ее построения используются две дополнительные формы функции step:

[y, t, x]= step(sys)

[y, t, x]= step(sys, t)

В этом случае функция step возвращает векторы значений выхода y, времени t и переменных состояния х (количество столбцов вектора х равно размерности lti-модели). Если модель представлена в tf или zpk формах, то параметр х опускается.

Пример 2.16.Расчет переходной характеристики с шагом 0.2 с без ее построения для непрерывной САУ с ПФ замкнутой системы Ф(s).

>> [y,t]=step(f,[0:0.2:4])

Задание 2.16. Произведите вычисление переходной функции дискретной системы с ПФ замкнутой САУ T(z) без ее построения.

Для расчета и построения импульсной переходной (весовой) характеристики используется функция impulse в таких же формах, как и функция step:

impulse (sys)

impulse (sys,t)

impulse (sys1, sys2,… ,sysN)

impulse (sys1, sys2,… ,sysN, t)

impulse (sys1, 'plotstyle1',… ,sysN, 'plotstyleN')

impulse (sys1, 'plotstyle1',… ,sysN, 'plotstyleN', t)

[y, t, x]= impulse (sys)

[y, t, x]= impulse (sys, t)

Пример 2.17.Построение весовой характеристики для линейной непрерывной САУ с ПФ замкнутой системы Ф(s) (рис. 2.7).

>>impulse(f); grid on

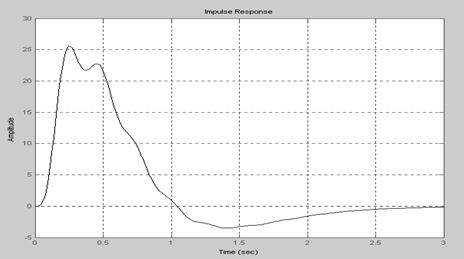
Рис. 2.7. Весовая характеристика

Задание 2.17.Постройте импульсную переходную характеристику для дискретной системы с ПФ замкнутой САУ Т(z).

Функция initial рассчитывает и строит график реакции ss-модели sys на ненулевые начальные условия. Она имеет несколько форм, эквивалентных функциям step и impulse:

initial (sys,х0)

initial (sys,х0,t)

initial (sys1, sys2,… ,sysN,х0)

initial (sys1, sys2,… ,sysN,х0, t)

[y, t, x]= initial (sys,х0)

[y, t, x]= initial (sys,х0, t)

Здесь х0 – вектор начальных условий lti-модели в пространстве состояний. Смысл остальных аргументов и возвращаемых величин такой же, как у функций step и impulse.

Пример 2.18.Построение реакции непрерывной системы, заданной математической моделью в пространстве состояний на единичное начальное условие по последней переменной состояния, т.е. х(0)=|0 0 0 0 0 0 1| (рис. 2.8).

>> sys 18=ss(f); x0=[0 0 0 0 0 0 1];initial(sys 18,x0); grid on

Задание 2.18.Постройте график реакции дискретной системы с исходной ПФ T(z) и представленной ss-моделью на единичное начальное условие по второй переменной состояния х(0)=|0 1 0 0 0 0 0|.

К блоку временных функций пакета Control System Toolbox относится еще две функции: lsim – вычисление переходного процесса при произвольном входном воздействии, который формируется с помощью функции gensig – генерация периодического сигнала заданного типа (синусоида, импульсная последовательность и прямоугольный периодический сигнал). Однако на практике они используются редко, так как для моделирования систем при сложных воздействиях более удобен пакет Simulink.

Дополнительное упражнение

1.Открыть mat-файл из созданного в результате выполнения дополнительного задания в разделе 1.

2.Используя lti-модели, полученные для разомкнутой и замкнутой непрерывной САУ, выполнить следующие виды работ.

2.1. Определить полюсы и нули замкнутой системы.

2.2. Осуществить сортировку полюсов и нулей.

2.3. Построить схему расположения нулей и полюсов на комплексной плоскости.

2.4. Произвести расчет собственных частот и коэффициентов демпфирования замкнутой системы.

2.5. Построить годограф Найквиста разомкнутой системы и оценить по нему устойчивость замкнутой системы.

2.6. Построить ЛЧХ разомкнутой системы и оценить запас устойчивости по фазе.

2.7. Определить запас устойчивости по модулю.

2.8. Рассчитать показатель колебательности системы.

2.9. Построить переходную характеристику системы.

2.10. Построить весовую характеристику системы.

3. Повторить пункты 2.1 ÷ 2.10 для дискретного варианта САУ.

Контрольные вопросы

1.Назовите основные функции, которые используются для анализа динамических параметров lti-моделей?

2.Поясните действие функций esort и dsort?

3.С помощью каких функций можно определить полюсы и нули динамической системы?

4.Какие основные функции используются для расчета и построения временных характеристик?

5.Каким образом рассчитываются временные характеристики без их построения?

6.Как задается время расчета переходного процесса?

7.Какие функции служат для построения частотных характеристик динамических систем?

8.Как реализовать логарифмическое изменения частоты?

9.Дайте сравнительную оценку функциям nyquist и bode.

10. С помощью какой функции строится схема расположения нулей и полюсов на комплексной плоскости?

11. Поясните особенности форм обращения к функции damp.

12. Как определить коэффициент передачи системы?

13. С помощью какой функции можно оценить запас устойчивости САУ?

14. Как рассчитать показатель колебательности системы?

15. Поясните особенности использования функции initial и задания в ней начальных условий.