Умножение двоичных чисел.
Умножение выполняется по тем же правилам , что и десятичное умножение, то есть перемножаются модули чисел, а знак результата получается сложением по модулю два знаков сомножителей.
Известно, что произведение двух n-разрядных чисел есть число 2n-разрядное
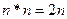
Возьмем два целых, четырёхразрядных двоичных числа
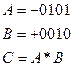 ( n = 4 )
( n = 4 )
 |
Знак произведения
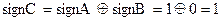 . Перемножаем модули
. Перемножаем модули
При умножении целых чисел в качестве результата берутся младшие n-разрядов. При этом в старших n-разрядах должны быть нули. Если это не так, то имеет место переполнение разрядной сетки машины. Для расширения разрядной сетки нужно добавить слева нули. Теперь умножим два дробных числа:
 |
При умножении дробных чисел в качестве результата выбираются старшие n-разрядов. При этом происходит округление по правилу: если в (n+1) разряде была единица, то к ответу добавляется единица в младший разряд, если в (n+1) разряде , был ноль, то к ответу ничего не добавляется. В примере имеем ноль, поэтому ничего не добавляем. Проверим ответ в десятичной системе:
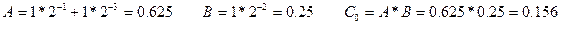
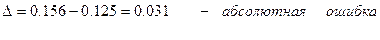
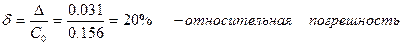
Округление при умножении дробных чисел вносит значительную погрешность (операции же с целыми числами выполняются абсолютно точно!).
Погрешность, возникающая при умножении дробных чисел равна
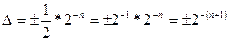
Чтобы не потерять точность при вычислениях, нужно расширить разрядную сетку путём добавления нулей справа.
Дата добавления: 2016-01-18; просмотров: 1266;
