Анализ геометрической структуры сооружений.

Сочленение двух дисков. Система может представлять собой сочленение отдельных неизменяемых частей (дисков), связанных между собой различно расположенными стержнями. Для анализа неизменяемости таких систем необходимо:

1) выделить неизменяемые части системы—диски;

2) провести анализ системы соединения дисков между собой.

Ниже остановимся на правилах соединения дисков начиная с простейшей системы двух дисков:

1. Сочленение двух дисков образует неизменяемую систему если диски связаны между собой тремя стержнями, осевые линии которых не пересекаются в одной точке или не параллельны между собой.

2. Соединение двух дисков составляет неизменяемую систему, если диски связаны шарниром и стержнем, причем центр шарнира не лежит на осевой линии стержня.

Схема соединения по первому признаку приведена на рис. 1.3.7 слева(1, 11 —Диски; 1 —3 - стержни).

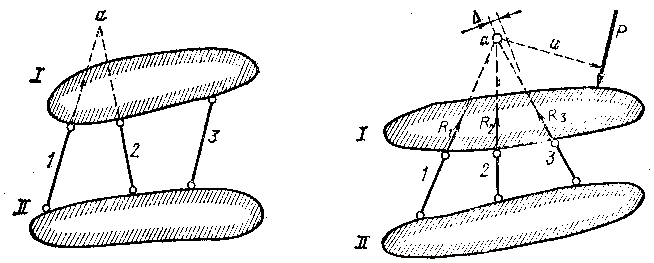
Рисунок 1.3.7.

При отсутствии стержня 3 возможно вращение дисков относительно точки а—мгновенного центра вращения; при наличии третьего стержня, осевая линия которого не проходит через точку «а» система неизменяема. Однако если три стержня пересекаются в одной точке (рис. 7 справа), система будет мгновенно изменяема, так как возможно бесконечно малое смещение диска путем вращения его вокруг мгновенного центра вращения а.

Фиктивные шарнир и стержень.

Отметим, что ненагруженный диск, шарнирно неподвижно присоединенный концами к остальной части конструкции, можно заменить стержнем, расположенным по оси диска и соединяющим концевые шарниры. Этот стержень называют заменяющим (фиктивным). Анализ неизменяемости и расчет ряда ферм при введении фиктивных стержней упрощается. Система по рис. 1.3.8 неизменяема: два диска 1 и 11 соединены двумя реальными стержнями 1 и 2 и третьим фиктивным стержнем 3, эквивалентным диску 111. Соединение дисков 1 и 11 двумя стержнями 1 и 2 можно заменить шарниром с. Рассмотрим подробнее эту систему в виде двух дисков 1 и 11, связанных между собой тремя стержнями 1, 2, 3, причем стержни 1 и 2 не соединены в точке пересечения их осевых линий (рис. 1.3.9).

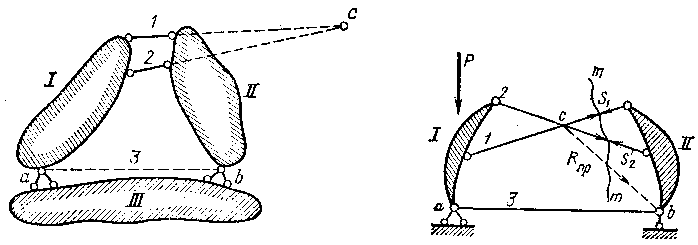
Рисунок 1.3.8 Рисунок 1.3.9.

Точка с в статическом и кинематическом отношении играет ту же роль, что и центр шарнирно неподвижной связи; равнодействующая R_пр усилий S₁ и S₂. в стержнях 1 и 2 должна проходить через точку их пересечения «с» аналогично реальному шарниру этой точке; перемещение диска 11 относительно диска 1 при наличии связи их только двумя стержням 1 и 2 совершается как вращение вокруг точки «с». Можно сформулировать следующее положение: связь двух дисков двумя стержнями с шарнирным прикреплением их концов к дисков эквивалентен соединению их шарниром с центром в точке пересечения осевых линий стержней.

Точку с в дальнейшем будем называть фиктивным шарниром. Схема системы по рис. 1.3.9, таким образом, сводятся к шарнирному треугольнику аbс, стороны которого соединяют реальные шарниры а, b и фиктивный шарнир с. В общем случае фиктивный стержень есть элемент, соединяющий фиктивные шарниры.

Используя принцип замены связей введением фиктивных шарниров и стержней можно упростить анализ неизменяемости большого класса сложных ферм.