Понятие о линии влияния.
Расчет сооружений на действие вертикальной подвижной нагрузки проводится с использованием линий влияния. Обычная подвижная нагрузка для мостов - движущийся железнодорожный состав (рис. 1.6.1) - представляет собой систему постоянных вертикальных сосредоточенных сил с неизменным расстоянием между грузами а1,а2,а3, …и т.д. Эта нагрузка движется по пролетному строению моста с известной скоростью v, занимая различные положения на сооружении. Аналогичны автомобильные и гусеничные нагрузки
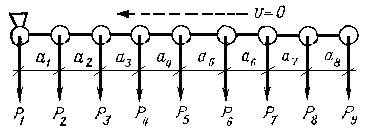
Рисунок 1.6.1
Решая статическую задачу, пренебрегают динамическим действием нагрузки, т.е.- исключают силы инерции, которые возбуждаются при вибрации самой балки и подвижного груза и не учитывают скорость движения груза. В динамике сооружений строятся динамические линии влияния, которые отражают наличие распределенных сил инерции сооружения и влияние скорости движения нагрузки.
Перейдем к получению статических линий влияния, применяя в каждый данный момент времени условия статического равновесия
Применяя принцип независимости изучают сначала действие лишь одного груза Р= 1, после чего легко получить значение усилия от груза поезда Р 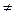 1, увеличивая усилие от единичного груза в Р раз.
1, увеличивая усилие от единичного груза в Р раз.
Линией влияния какого-либо усилия для определенного сечения сооружения называется графическое изображение закона изменения данного усилия в этом сечении при перемещении груза Р= 1 по длине сооружения.
Линия влияния представляет собой диаграмму, при построении которой функцией является изучаемая величина усилия, а независимой переменной — абсцисса груза Р= 1. Каждая ордината линии влияния численно равна значению изучаемого усилия для положения груза на сооружении над этой ординатой.
При построении линии влияния сечение неподвижно, положение груза меняется; при построении эпюры моментов меняется положение сечения, нагрузка неподвижна.
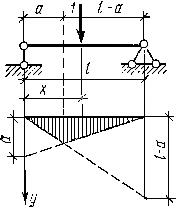
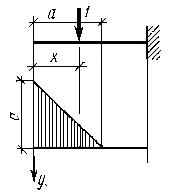
Рисунок 1.6.2 Рисунок 1.6.3
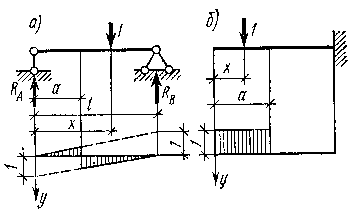
Рисунок 1.6.4
Нетрудно построить линии влияния усилий в простых статически определимых балках. Например, линию влияния изгибающего момента в сечении, расположенном на расстоянии а от левой опоры однопролетной балки, изображает график функции:
Ма=(l—а)х/l при 0 <x < a ;
Ма= а (l— х)/l при а <x < 1,
где 1- пролет балки (рис. 1.6.2).
Действительно, опорные реакции балки при единичной сосредоточенной силе, приложенной на расстоянии х от левой опоры, равны:
Ra= (l-x)/l , Rb=x/l
Для сечений, расположенных слева от точки приложения сил (а <x), изгибающий момент Ма = Ra а, а для сечений, расположенных справа от этой точки (a > x): Ма = Rb(l-а). Линия влияния здесь имеет вид треугольника с вершиной в заданном сечении а. Максимальная ордината линии влияния при х= а
Мmax = (l-a)a/l.
Линия влияния изгибающего момента в консольной балке (рисунок 1.6.3) для сечения, находящегося на расстоянии а от свободного конца, выражается формулами
Ма=х-а при x < a
Ма=0 при x > a
Легко построить также линии влияния поперечной силы в произвольной точке, находящейся на расстоянии а от левого конца однопролетной или консольной балки. Эти линии влияния выражаются уравнениями:
для однопролетной балки (рис. 1.6.4, а)
Qa= - Rb= -x/l при х<а;
Qa=Ra = (l-x)/l при х>a.
для консольной балки (рис. 1.6, 6)
Qa= 1 при х<а;
Qa= 0 при х>a.
При х = а линии влияния поперечных сил имеют разрыв на величину, равную единице.
Несколько сложнее построение линий влияния усилий в элементах статически определимых форм, арок и других систем. Еще более сложными методами строятся линии влияния и элементах статически неопределимых систем. В общем случае ординаты линий влияния можно вычислить по точкам, прилагая каждый раз единичную силу в соответствующей точке и определяя рассматриваемое усилие обычным расчетом. Заметим, что линии влияния усилий в статически определимых системах при движении груза по прямой изображаются отрезками прямых линий, в то время как линии влияния усилий в статически неопределимых системах, как правило, криволинейные.
Дата добавления: 2016-01-18; просмотров: 1589;
