Распределение электронов в атоме по состояниям

Квантовые числа

Итак, из решения уравнения Шредингера для электрона, находящегося в атоме, следует, что его энергия W_n, а значит и импульс p_n и волновое число k_n не могут быть любыми, они квантуются.

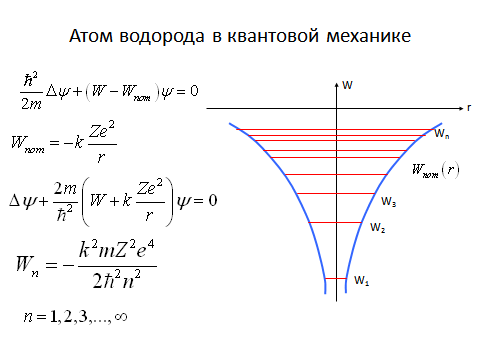
Поэтому и волновая функция, описывающая поведение каждого электрона, находящегося в разных состояниях, должна быть разной даже для одного электрона.

Так как электрон в атоме обладает значительными волновыми свойствами

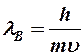m ~ 10^-30 м, u₁ ~ 10⁶ м/с.

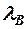~ 10^-10 м~размер атома !

поэтому его нельзя рассматривать в виде частицы, понятие «траектория движения» = «орбита электрона» неприменимы!

Зная, что квадрат модуля волновой функции определяет вероятность нахождения электрона в атоме, можно представлять электрон в виде некоторого отрицательно заряженного облака, имеющего разную форму в зависимости от его состояния.

Для описания с помощью волновой функции поведения конкретного электрона, находящегося в атоме в разных состояниях, используются квантовые числа:

1. Главное квантовое число n, которое определяет значение энергии электрона в атоме

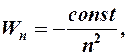n = 1, 2, 3, …, ¥

2. Орбитальное (азимутальное) квантовое число 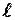, которое определяет форму электронного облака (форму электронной орбитали).

Электронная орбита ® электронная орбиталь !!!

Так как электрон в атоме находится в непрерывном движении, то он обладает орбитальным моментом импульса L, который так же как и энергия, квантуется

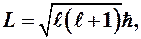(9-1)

где 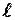= 0, 1, 2, 3, …, n – 1.

В спектроскопии электронным орбиталям различной формы (с разным орбитальным квантовым числом 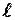) сопоставимы свои обозначения

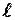= 0, 1, 2, 3, …, n – 1

s p d f ……

3. Магнитное квантовое число m, которое характеризует ориентацию электронной орбитали в пространстве по отношению к какому-либо направлению (например, по отношению к направлению внешнего магнитного поля).

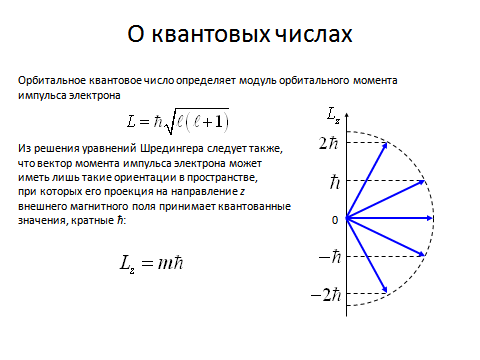
Если классическая электродинамика считала, что момент импульса электрона может быть произвольно ориентирован по отношению к любому направлению (например, к направлению внешнего магнитного поля), то квантовая механика (это следует из решения уравнения Шредингера) утверждает, что вектор момента импульса электрона может иметь только такие ориентации в пространстве, при которых его проекции на направление внешнего магнитного поля принимают квантовые значения, кратные постоянной Планка:

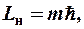(9-2)

где m = 0, ±1, ±2, …, ± ,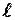

т. е. всего 2 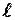+1 значений.

Хотя энергия электрона и зависит только от главного квантового числа n, но каждому собственному значению энергии W_n (кроме W₁) соответствует несколько волновых функций 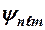, отличающихся значением 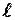и m.

Следовательно, атом может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

Согласно квантовой механике каждому энергетическому состоянию соответствует своя волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема атома.

Вероятность обнаружения электрона в разных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках объема атома.

Квантовые числа n и 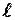характеризуют размер и форму электронного облака, а квантовое число m характеризует ориентацию электронного облака в пространстве.

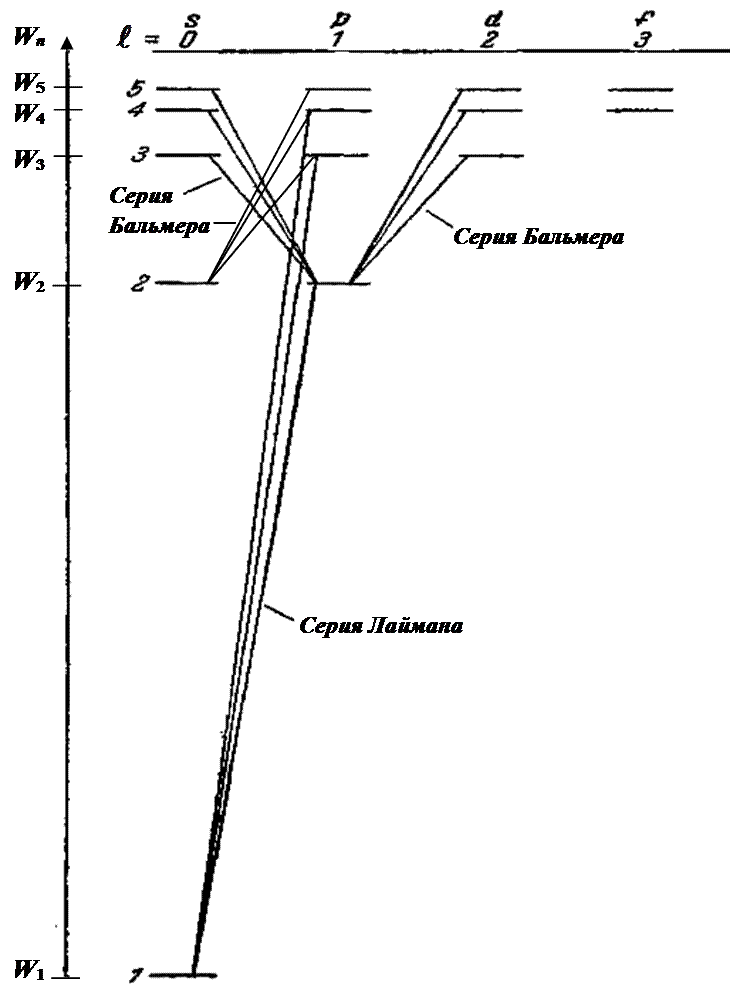
Квантовые числа n, 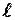, и m позволяют точнее описать спектр испускания (поглощения) атома (в частности, атома водорода, описанный в теории Бора).

В квантовой механике вводятся правила отбора,ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света.

Теоретически доказано и экспериментально подтверждено, для электрона в атоме могут осуществляться только такие переходы, для которых:

1) орбитальное квантовое число 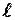изменяется только на единицу

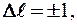
2) изменение магнитного квантового числа m удовлетворяет условию

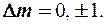
С учетом этого спектральные серии линий излучения атома водорода должны соответствовать переходам:

4. Согласно законам классической механики электрон, двигаясь в атоме, обладает не только орбитальным моментом импульса 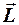, но и магнитным моментом 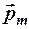, направленным .

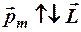Отношение магнитного момента электрона в атоме 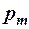к орбитальному моменту импульса L называется гиромагнитным отношением

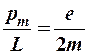(9-3)

где e – электрический заряд электрона,

m – масса электрона.

Но эксперименты, проведенные Эйнштейном и де Гаазом, по измерению гиромагнитного отношения дали результат вдвое больший:

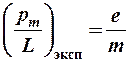(9-4)

? ? ?

Более того, Штерн и Герлах, проведя прямые измерения магнитных моментов, обнаружили, что узкий пучок атомов водорода, заведомо находящийся в основном состоянии 1s, в неоднородном магнитном поле расщепляется на два пучка.

В этом состоянии 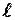= 0, поэтому момент импульса, а значит и магнитный момент такого электрона (атома водорода) равен нулю и магнитное поле не должно оказывать влияние на движение атомов водорода в основном состоянии, т.е. расщепления быть не должно.

Однако эксперимент показал, что в s-состоянии даже в отсутствие внешнего магнитного поля, существует расщепление.

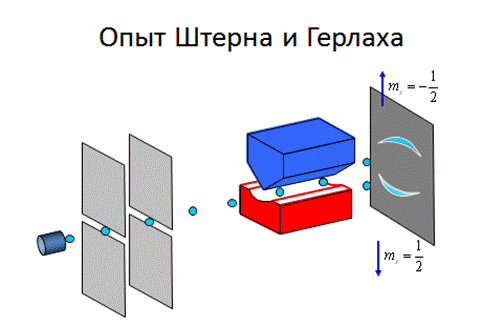
Для объяснения этого факта, американские физики Уленбек и Гауд-смит предположили, что электрон обладает кроме орбитальных момента импульса и магнитного момента, еще и собственным неуничтожимым механическим моментом импульса – спином L_sи собственным магнитным моментом 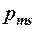, которые тоже квантуются:

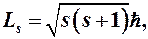(9-5)

где s – спиновое квантовое число (для электрона s = ).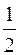

Проекция 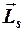на направление внешнего магнитного поля удовлетворяет условию:

где m_s – магнитное спиновое квантовое число (для электрона m_s может принимать только два значения ).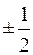

Т.о. для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще и магнитное спиновое квантовое число.

.

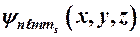Распределение электронов в атоме по состояниям

Распределение электронов в любом атоме по состояниям подчиняется принципу минимума энергии:

- наиболее выгодное энергетическое состояние для электрона в атоме – это состояние с минимальной энергией.

Далее электроны занимают свободные состояния в соответствии с набором четырех квантовых чисел n, 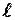, m и m_s.

Кроме того, распределение электронов в атоме подчиняется принципу запрета Паули:

- в одном и том же атоме не может быть даже двух электронов с одинаковым набором всех четырех квантовых чисел.

Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме, различаются значениями по крайней мере одного квантового числа.

Максимальное количество электронов, находящихся в состояниях, определяемых данным главным квантовым числом, равно

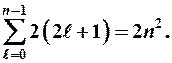(9-6)

Кроме того при заполнении различных состояний электронами руководствуются правилом Хунда (Гунда):

­¯ ­ ¯

нет да

Пример:атом натрия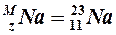

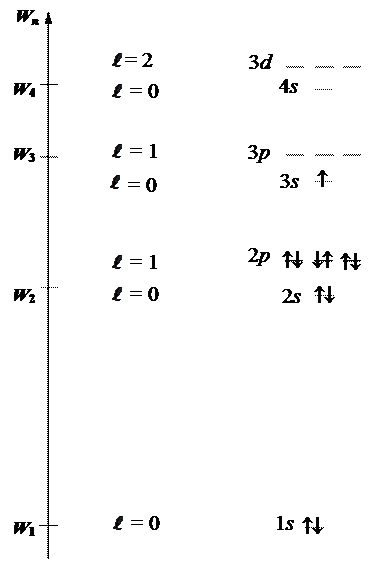ряд Клечковского

Na: 1s²2s²2p⁶3s¹

Совокупность электронов в многоэлектронных атомах, имеющих одно и то же главное квантовое число n, называется электронной оболочкой (K, L, M, N, …).

В каждой из оболочек электроны распределяются по подоболочкам, соответствующим данному .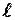

Таблица

Главное квантовое число n
Символ оболочки	K	L	M
Максимальное число электронов в оболочке
Орбитальное квантовое число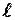
Символ подоболочки	1s	2s	2p	3s	3p	3d
Максимальное число электронов в подоболочке