Энергетические уровни
Теория водородоподобного атома.
В переводе с греческого языка «атом» - это неделимая частица, это тот первокирпичик, из которых построена вся материя, все вещества.

Однако простая ионизация атома, при которой нейтральный атом становится положительно заряженным ионом, и при этом из атома вылетает отрицательно заряженный электрон, указывает на сложное строение атомов.
(Ионизация атома – процесс отрыва электрона от атома и превращение атома в положительно заряженный ион.)
Значит, атом имеет сложное строение!
Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит английскому физику Томсону (1903 г.)
Согласно этой модели, атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10-10 м, внутри которого около своих положений равновесия колеблются электроны; суммарный отрицательный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален – модель «пудинг с изюмом»!
Однако довольно быстро было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно.

В 1919 году английский физик Резерфорд провел опыты по бомбардировке a-частицами атомов, в результате которых была создана так называемая «планетарная модель атома»: в центре атома находится положительно заряженное ядро, в котором сосредоточена практически вся масса атома, а вокруг ядра, подобно планетам Солнечной системы, движутся по орбитам отрицательно заряженные электроны (их суммарный заряд по модулю равен заряду ядра – так что в целом атом нейтрален).
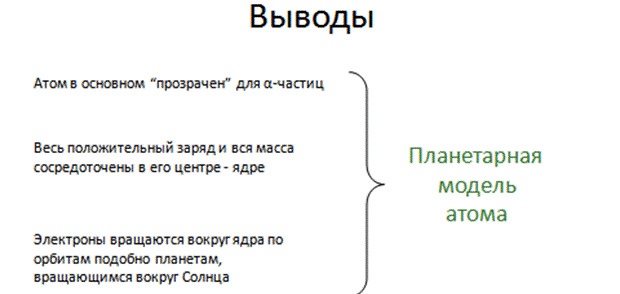

Критика планетарной модели:
1) Электрон – заряженная частица, движется с центростремительным ускорением, а из электродинамики известно, что заряженная частица, движущаяся с ускорением, излучает электромагнитные волны.
Тогда, потеряв энергию на излучение, электрон должен быть электрической силой притянут к ядру и атом должен прекратить свое существование.
Но этого не происходит. Атомы существуют вечно!
2) Если электрон непрерывно теряет свою энергию, значит, атом должен излучать энергию на всех частотах, но эксперименты показывают, что спектр излучения атомов – линейчатый.
Классическая физика не смогла объяснить эти противоречия.
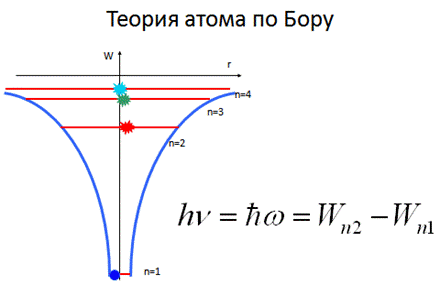
Спасти ситуацию попытался датский физик-теоретик Нильс Бор, который ввел понятие «квантование электронных орбит», сформулировав два постулата:
Первый постулат Бора (постулат стационарных состояний):в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
В стационарном состоянии атома электрон, двигаясь по круговой орбите с центростремительным ускорением, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию:
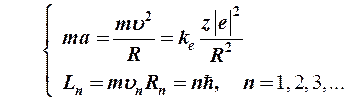 (8-1)
(8-1)

Решая эту систему уравнений, Бор получил выражения для радиусов электронных орбит, скорости и энергии электронов на этих орбитах, которые представляют дискретный набор значений:
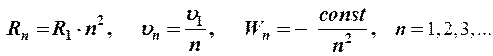 , (8-2)
, (8-2)
где R1 = 0,53×10-10 м - радиус первой боровской орбиты,
u1 = 2,19×106 м/с – скорость электрона на первой орбите,
const – постоянная для каждого атома (для атома водорода const = 13,6 эВ).
Второй постулат Бора (постулат частот): при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
hn = Wm – Wn , (8-3)
равной разности энергий соответствующих стационарных состояний до и после излучения (поглощения).
Набор возможных дискретных частот, определяемый квантовыми переходами (8-3) и определяет линейчатый спектр атома.
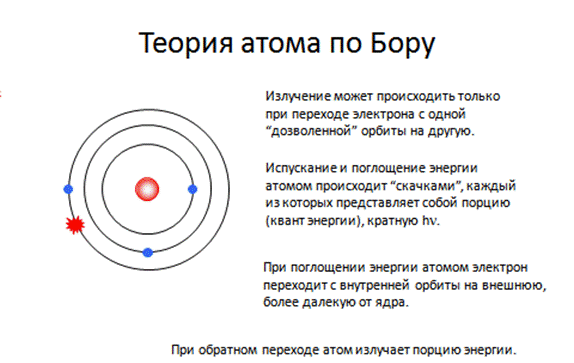

Боровская теория смогла описать излучение лишь водородоподобных атомов!
А для остальных результаты сильно расходились с экспериментом.
Спасти ситуацию попытался Зоммерфельд. Он рассуждал примерно так: электрон = волна де Бройля, для которой должно выполнятся условие: на длине орбиты должно укладываться целое число длин волн
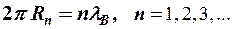
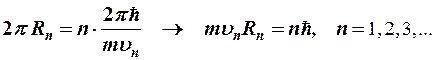 ,
,
что соответствует условию квантования боровских орбит (см. формулу (8-1)).
Ответ на все вопросы дала лишь квантовая механика.
Потенциальная энергия взаимодействия электрона с ядром атома представляет собой гиперболическую функцию
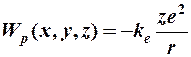 ,
,
тогда уравнение Шредингера запишется в виде:
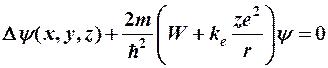 .
.
Решая его относительно энергии частицы W, получим:
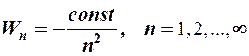 (8-4)
(8-4)
где для атома водорода const = 13,6 эВ.
 |
Состояние с n = 1 – основное (невозбужденное) состояние.
Из соотношения неопределенностей Гейзенберга
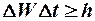
следует, что если 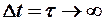 , то
, то 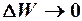 .
.
Все остальные состояния с n = 2,3, …, ¥ - возбужденные.
Чтобы электрон из основного состояния перешел в любое возбужденное состояние, ему нужно сообщить дополнительную энергию
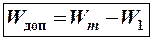 (8-5)
(8-5)
где W1 – энергия основного состояния (для атома водорода W1 = -13,6 эВ),
Wm – энергия возбужденного состояния, куда переходит электрон (атом).
Если электрону, находящемуся в основном состоянии, сообщить дополнительную энергию, достаточную для перехода его в состояние с W¥ =0, то это равносильно процессу отрыва электрона от атома – ионизация!
Следовательно, минимальная энергия, которую нужно сообщить невозбужденному атому, чтобы он стал положительно заряженным ионом, - энергия ионизации равна
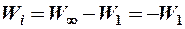 ,
,
для атома водорода Wi = 13,6 эВ.
В любом возбужденном состоянии электрон находится очень короткое время t ~ 10-8 c. За это время он теряет часть своей энергии и переходит в состояние с меньшей энергией.
Потеря электроном атома энергии при переходе его из состояния с большей энергией Wm в состояние с меньшей энергией Wn сопровождается электромагнитным излучением = испускается фотон, энергия которого
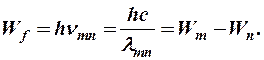 (8-6)
(8-6)
где Wm – энергия состояния, с которого переходит электрон;
Wn – энергия состояния, на которое переходит электрон.
Из (8-6) получаем:
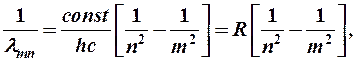 (8-7)
(8-7)
где R = 1,097×107 м-1 – постоянная Ридберга.
Каждому переходу m ® n соответствует своя спектральная линия lmn.
Так как время жизни электрона в возбужденном состоянии составляет t ~ 10-8 c, тогда, воспользовавшись соотношением неопределенностей Гейзенберга можно получить оценку ширины возбужденного энергетического уровня:
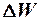 ~ 10-7 эВ
~ 10-7 эВ
 Так как
Так как 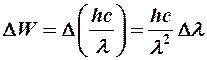 ® отсюда можно оценить Dl - естественную ширину спектральной линии.
® отсюда можно оценить Dl - естественную ширину спектральной линии.
   | |||
 |
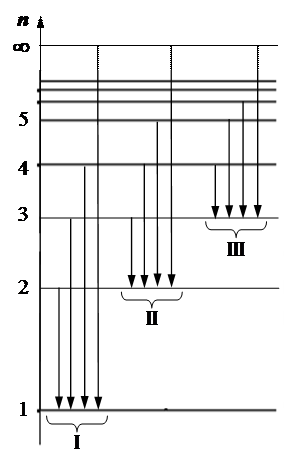
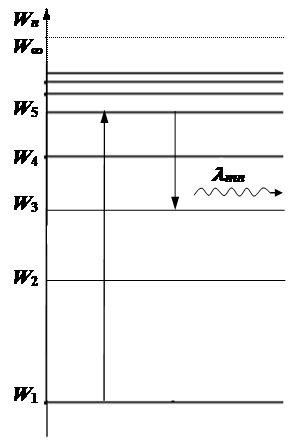
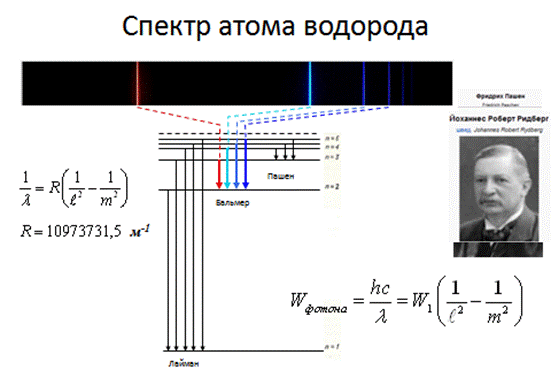
Спектральная серия линий– группа спектральных линий, соответствующая излучению возбужденных атомов при переходах электронов с вышележащих уровней на один нижележащий.
При переходе с m = 2, 3, …, ¥ на уровень n = 1 ® l mn < lф = 400 нм – ультрафиолетовая область излучения – серия Лаймана.
При переходе с m = 3, 4, …, ¥ на уровень n = 2 ® 400 нм < lmn < 700 нм – видимый свет – серия Бальмера.
При переходе с m = 4, 5, …, ¥ на уровень n = 3 ® lmn > lкр = 700 нм – инфракрасная область излучения – серия Пашена.
В любой спектральной серии есть lmin и lmax
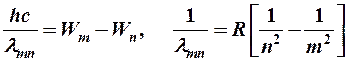
Максимальной энергии излученного фотона 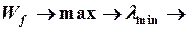 , что соответствует переходу электрона с уровня m = ¥ на уровень с номером n.
, что соответствует переходу электрона с уровня m = ¥ на уровень с номером n.
Минимальной энергии излученного фотона 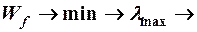 , что соответствует переходу электрона с соседнего уровня m = n + 1 на уровень с номером n.
, что соответствует переходу электрона с соседнего уровня m = n + 1 на уровень с номером n.


Задача: Какую дополнительную минимальную энергию нужно сообщить невозбужденному атому водорода, чтобы в его излучении появилась хотя бы одна видимая линия?
Видимая линия ® серия Бальмера
Хотя бы одна ® l32 переход 3 ® 2
Значит, чтобы она появилась, нужно возбудить невозбужденный атом водорода, переведя его из основного состояния с n = 1 в возбужденное с n = 3, тогда
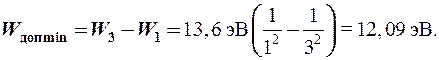
| <== предыдущая лекция | | | следующая лекция ==> |
| Квантовая частица в одномерной | | | Распределение электронов в атоме по состояниям |
Дата добавления: 2016-01-18; просмотров: 1641;
