ОСОБЫЕ СЛУЧАИ НЕСИММЕТРИИ В ТРЁХФАЗНЫХ ЦЕПЯХ
Рассматриваются простейшие трёх- и четырёхпроводные цепи генератор-приёмник с соединением фаз приёмника и генератора в звезду и треугольник. К особым случаям несимметрии относят обрывы проводов и фаз, короткие замыкания фаз, если исходная схема работает в симметричном режиме. В этом случае цепь перестаёт быть симметричной, однако имеет место ряд особенностей, облегчающих расчёт.
ЗАДАЧА 4.21. Для симметричной трёхфазной системы «звезда-звезда без нулевого повода» (рис. 4.27,а) рассчитать режимы работы следующих случаев: - симметричный режим;
- обрыв линейного провода А;
- короткое замыкание фазы А.
Параметры схемы: U = 380 В, r = x = 20 Ом.

Решение
На рис. 4.27,б приведена векторная диаграмма симметричного режима системы Y-Y. При этом напряжение между нулевыми точками симметричной системы UN = 0.
Фазные ЭДС генератора и фазные напряжения приёмника
EA = UA =  =
= 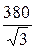 = 220 B; EB = UB = 220×e –j120° B; EC = UC = 220×e j120° B;
= 220 B; EB = UB = 220×e –j120° B; EC = UC = 220×e j120° B;
а также токи IA =  =
= 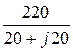 = 7,78×e –j45° А;
= 7,78×e –j45° А;
IВ = IA×e –j120° = 7,78×e –j165° А; IС = IA×e j120° = 7,78×e j75° А
образуют симметричные системы векторов.
При обрыве линейного провода А последовательно с сопротивлением этой фазы Z = r + jx = 20 + j20 Ом можно считать включенным дополнительное сопротивление обрыва Zобр = ¥, при этом сопротивление ветви А становится равным ZА = Zобр + Z = ¥. Узловое напряжение (его называют напряжением смещения нейтрали)
UN = 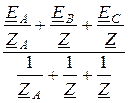 =
= 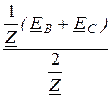 = -
= - 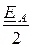 = -
= - 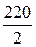 = -110 B.
= -110 B.
При подсчёте учтено, что при обрыве провода А проводимость  =
= 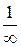 = 0, отношение
= 0, отношение  =
= 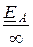 = 0, и в симметричной системе
= 0, и в симметричной системе
EA + EB + EC º 0, откуда EB + EC = -EA.
Напряжение на сопротивлении ZА UA = EA – UN = 1,5×EA = 330 B
является напряжением между точками обрыва провода А, а ток оборванного провода IA =  =
= 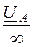 = 0.
= 0.
Напряжения и токи неповреждённых фаз
UB = EB – UN = 220×e –j120° +110= -j190 B; IB = 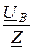 =
=  = 6,72×e –j135° A;
= 6,72×e –j135° A;
UC = EC – UN = 220×e j120° +110= j190 B; IC = 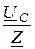 =
= 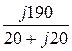 = 6,72×e j45° A.
= 6,72×e j45° A.
Заметим, что при обрыве линейного провода трёхфазная цепь превращается в однофазную, поэтому токи неповреждённых фаз можно найти и более простым способом: IB = -IC = 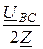 =
= 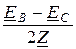 .
.
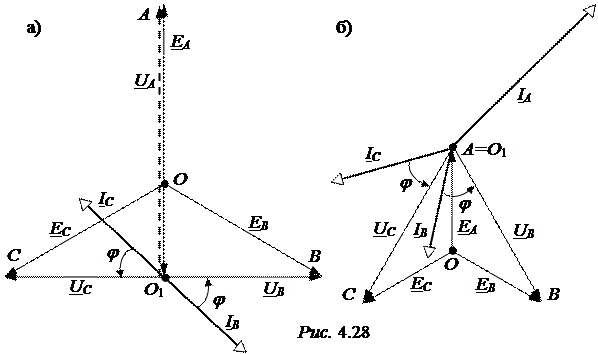 |
Векторная диаграмма рассматриваемой системы Y-Y без нулевого провода при обрыве линейного провода А приведена на рис. 4.28,а.
Сравнивая напряжения на фазах неповреждённых фаз при обрыве провода А (UB = UC = 190 В) и при работе в симметричном режиме, когда все напряжения UA = UB = UC = 220 В, отмечаем уменьшение напряжения на 13,7%, что недопустимо для питания осветительной нагрузки.
Расчёт схемы при коротком замыкании фазы А осуществляется по общему правилу расчёта разветвлённой цепи с выполнением предельного перехода при ZA ® 0:
UN = 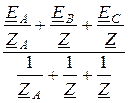 =
= 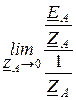 = EA.
= EA.
Напряжения и токи неповреждённых фаз
UB = EB – UN = EB – EA = -UAB = -380×e j30° = 380×e –j150° B;
IB = 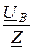 =
= 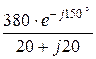 = 13,44×e –j195° A;
= 13,44×e –j195° A;
UC = EC – UN = EC – EA = UCB = 380×e j150° B;
IC = 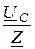 =
=  = 13,44×e j105° A.
= 13,44×e j105° A.
Ток короткозамкнутой фазы
IA =  =
=  =
= 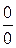 = -(IB + IC) = -
= -(IB + IC) = - 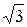 IC ×e j30°= -23,3×e j135°= 23,3×e –j45° A.
IC ×e j30°= -23,3×e j135°= 23,3×e –j45° A.
выражение для IA получено из условия, что для трёхпроводной системы IA + IB + IC = 0.
Векторная диаграмма цепи при коротком замыкании фазы А приведена на рис. 4.28,б.
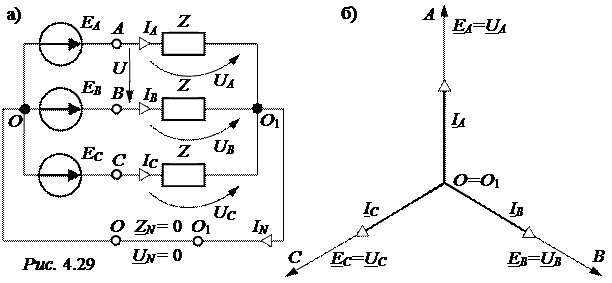
ЗАДАЧА 4.22. Для симметричной системы «звезда-звезда с нулевым проводом» (ZN = 0) (рис. 4.29,а) выполнить расчёты для трёх случаев:
- симметричный режим;
- обрыв линейного провода В;
- короткое замыкание фазы В, если: U = 220 В, Z = r = 20 Ом.
Решение
На рис. 4.29,б приведена векторная диаграмма для симметричного режима работы схемы, в которой UN = 0 из-за нулевого значения сопротивления ZN .
При этом фазные напряжения генератора и нагрузки одинаковы и в 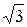 раз меньше линейных напряжений: UФ = E =
раз меньше линейных напряжений: UФ = E =  =
=  = 127 B.
= 127 B.
Примем EA= UФ = 127 B, тогда EB= 127×e -j120° B, EС= 127×e j120° B;
 |
IA =
 =
= 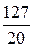 = 6,35 А; IВ = IA×e –j120° = 6,35×e –j120° А; IС = IA×e j120° = 6,35×e j120° А.
= 6,35 А; IВ = IA×e –j120° = 6,35×e –j120° А; IС = IA×e j120° = 6,35×e j120° А.
При обрыве линейного провода B можно считать, что последовательно с сопротивлением Z в фазу B подключилось сопротивление обрыва Zобр = ¥ и
полное сопротивление ветви стало ZВ = Z + Zобр = ¥.
По II закону Кирхгофа для контуров «ветвь – нулевой провод» получаем при обрыве провода B:
IA =  =
= 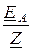 =
= 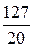 = 6,35 А – то же значение, что и при симметричном режиме,
= 6,35 А – то же значение, что и при симметричном режиме,
IВ =  =
= 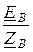 =
=  = 0;
= 0;
IС = 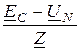 =
= 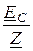 =
= 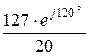 = 6,35×e j120° А – то же значение, что и при симметричном режиме.
= 6,35×e j120° А – то же значение, что и при симметричном режиме.
Ток нулевого провода
IN = IA + IВ + IС = 6,35 + 0 + 6,35×e j120° = -6,35×e -j120° = 6,35×e j60° А.
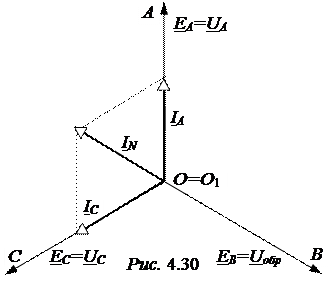 Заметим, что IN = -IВ сим. По этому поводу говорят, что нулевой провод воспринимает на себя ток оборванной фазы. Векторная диаграмма цепи при обрыве провода B приведена на рис. 4.30.
Заметим, что IN = -IВ сим. По этому поводу говорят, что нулевой провод воспринимает на себя ток оборванной фазы. Векторная диаграмма цепи при обрыве провода B приведена на рис. 4.30.
 |
При коротком замыкании фазы B в четырёхпроводной системе ток короткозамкнутого контура EB - ZB - ZN неограниченно возрастает. Такой режим называется аварийным. Для защиты от такого аварийного режима в линейный провод B (и в остальные линейные провода) включаются плавкие предохранители, отключающие аварийную фазу (перегорают), после чего схема переходит в режим работы с оборванной фазой B (рис. 4.29).
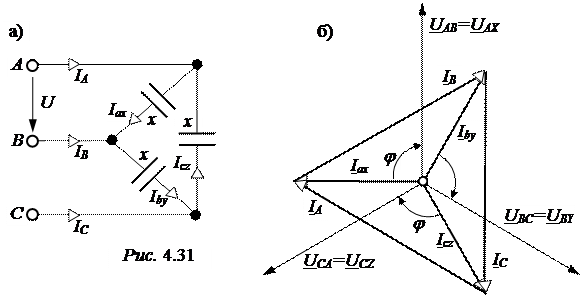
ЗАДАЧА4.23. Рассчитать режим работы симметричного треугольника (рис. 4.31,а) при U = 660 В, xC = 100 Ом для четырёх случаев:
- симметричный режим;
- обрыв линейного провода С;
- обрыв фазы СZ;
- короткое замыкание фазы СZ.
Решение
Примем UAB = U = 660 B.
При соединении фаз нагрузки в треугольник его линейные напряжения равны фазным напряжениям. В симметричном режиме получаем
UAX = UAB = 660 B, UBY = UBC = 660×e -j120° B, UCZ = UСA = 660×e j120° B.
Фазные токи треугольника
Iах =  =
= 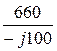 = j6,6 = 6,6×e j90° А;
= j6,6 = 6,6×e j90° А;
Iby = 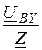 = Iах ×e –j120° = 6,6×e –j30° А; Icz =
= Iах ×e –j120° = 6,6×e –j30° А; Icz =  = Iах ×e j120° = 6,6×e j210° А.
= Iах ×e j120° = 6,6×e j210° А.
Линейные токи треугольника
IA = Iах – Icz = 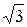 Iах ×e –j30° = 11,4×e j60° А;
Iах ×e –j30° = 11,4×e j60° А;
IВ = IA×e –j120° = 11,4×e –j60° А; IС = IA×e j120° = 11,4×e j180° = -11,4 А.
Векторная диаграмма симметричного треугольника приведена на рис. 4.31,б. При обрыве линейного провода С все токи и напряжения нагрузки определяются только линейным напряжением UAB.
Ток Iах =  =
= 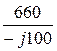 = j6,6 А - прежний.
= j6,6 А - прежний.
Ток IС = 0, так как провод С оборван, токи
Iby = Icz = - 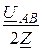 = -
= - 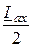 = -j3,3 А,
= -j3,3 А,
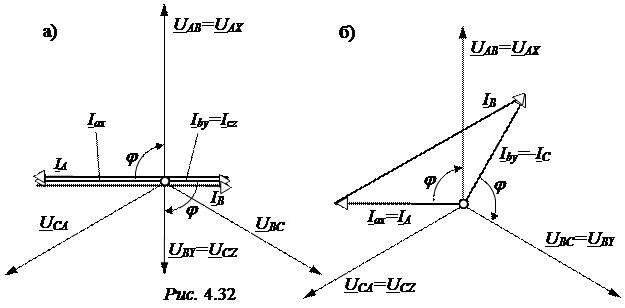
напряжения на фазах UВY = UСZ = Iby ×Z = - 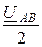 = -330 B.
= -330 B.
Линейные токи IA = Iax – Icz = 1,5×Iax = j9,9 А;
IВ = Iby – Iax = -1,5×Iax = -j9,9 А.
Векторная диаграмма треугольника сопротивлений при обрыве линейного провода С приведена на рис. 4.32,а.
При обрыве фазы СZ её ток Icz = 0, а токи фаз
Iax = j6,6 А, Iby = 6,6×e –j30° А такие же, как и в симметричном режиме.
Линейный ток IA = Iax – Icz = Iax = j6,6 А, линейный ток IВ = Iby – Iax = 11,4×e –j60° А тот же, что и в симметричном режиме, линейный ток IС = -Iby = 6,6×e j150° А.
Векторная диаграмма цепи при обрыве фазы СZ приведена на рис. 4.32,б.
При коротком замыкании фазы СZ в контуре «А – короткозамкнутая фаза СZ – В – источник питания» нет сопротивлений, и ток неограниченно возрастает, создавая аварийный режим работы, что требует отключения от сети проводов А или С.
ЗАДАЧА4.24. Трёхфазный приёмник, фазы которого соединены в звезду, включен на напряжение 380 B. Мощность и коэффициент мощности приёмника Рном = 11,9 кВт, cosj = 0,72. Выполнить следующее:
- нарисовать схему цепи и определить сопротивление фазы приёмника ZНГ;
- нарисовать схему цепи, построить векторную диаграмму при обрыве B-фазы и указать, как изменится мощность приёмника в сравнении с номинальной;
- нарисовать схему цепи, построить векторную диаграмму при коротком замыкании B-фазы и указать, как изменится мощность приёмника в сравнении с номинальной.
Ответы: ZНГ = 6,3 + j6,1 Ом; уменьшится вдвое; возрастёт вдвое.
ЗАДАЧА 4.25. Трёхфазный приёмник, фазы которого соединены в треугольник, включен на напряжение 220 B. Мощность коэффициент мощности приёмника Рном = 11,9 кВт, cosj = 0,72. Выполнить следующее:
- нарисовать схему цепи и определить сопротивление фазы приёмника ZНГ;
- нарисовать схему цепи, построить векторную диаграмму при обрыве B-фазы и указать, как изменится мощность приёмника в сравнении с номинальной;
- нарисовать схему цепи, построить векторную диаграмму при обрыве питающего провода B и указать, как изменится мощность приёмника в сравнении с номинальной.
Ответы: ZНГ = 6,3 + j6,1 Ом; уменьшится на одну треть; уменьшится вдвое.
Дата добавления: 2016-01-18; просмотров: 2210;
