Если распределение признака близко к нормальному или симметричному распределению, то или .

В условияхнормального распределениясуществует следующая взаимосвязь между величиной среднего квадратического отклонения 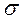и количеством наблюдений:

- в пределах 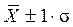располагается 68,3% количества наблюдений;

- в пределах 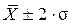располагается 95,4%;

- в пределах 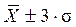располагается 99,7% количества наблюдений.

Это положение называютправилом трех сигм.

Коэффициент осцилляции – процентное отношение размаха вариации к средней величине признака.

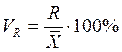
Линейный коэффициент вариации – процентное отношение среднего линейного отклонения к средней величине признака.

Коэффициент вариации – процентное отношение среднего квадратического отклонения к средней величине признака, т.е. это относительный показатель вариации признака.

В этой связи валидной мерой вариабельности асимметричного распределения социально-экономических показателей является среднее квадратическое отклонение.

Совокупность считается однородной, если коэффициент вариации не превышает 33%(для распределений, близких к нормальному). Различают следующие коэффициенты вариации.

Для альтернативных признаков: 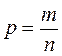- доля единиц совокупности, обладающих данным признаком; - доля единиц, не обладающих данным признаком. Дисперсия альтернативного признака: .

Общая дисперсия ( 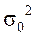) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию.

Межгрупповая дисперсия ( 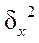) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под действием признака-фактора, положенного в основу группировки.

;

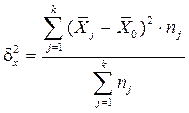где - число групп;

- число единиц в j-й совокупности;

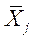- частная средняя по j-й группе;

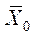- общая средняя по совокупности единиц.

Внутригрупповая дисперсия ( ) отражает случайную вариацию, т.е. часть вариации, происходящей под влиянием неучтенных факторов и не зависящую от признака-фактора.

.

По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий ( ):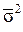

.

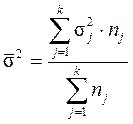Общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий:

.

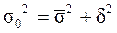Эмпирический коэффициент детерминации – доля межгрупповой дисперсии в общей дисперсии.

.

Эмпирическое корреляционное отношение – корень квадратный из эмпирического коэффициента детерминации (если 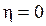, то группировочный признак не оказывает влияния на результативный; если же , то результативный признак изменяется только в зависимости от признака, положенного в основу группировки, а влияние прочих факторных признаков равно нулю):

.

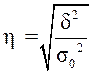Для проверки существенности связи между группировочным признаком и вариацией исследуемого признака часто используется дисперсионное отношение (критерий Фишера).

,

где , 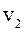- число степеней свободы для сравниваемых дисперсий,

при этом ;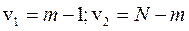

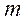- число групп;

- число наблюдений.

Расчетное значение критерия Фишера ( 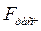) сравнивается в критическим ( 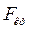), которое определяется по таблице; если , наличие связи доказано.

В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место в ранжировано вариационном ряду.

Квартили – значения признака, делящие ранжированную совокупность на четыре равновеликие части нижний квартиль ( 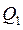) отделяет часть совокупности с наименьшим значением признака; верхний квартиль ( 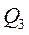) отсекает часть с наибольшими значениями признака.

Децили – значение признака, делящие ранжированную совокупность на десять равных частей.

Перцентили – значения признака, делящие ранжированную совокупность на сто равных частей.

Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанном с изменением вариант; кривую распределения применяют в качестве обобщающей характеристики особенностей формы распределения.

Нормальное распределение – это распределение, в котором средняя арифметическая, мода и медиана равны между собой. Формула функции плотности нормального распределения такова:

.

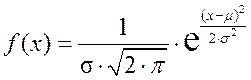Следовательно, кривая нормального распределения может быть построена по двум параметрам – средней арифметической 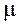и среднему квадратическому отклонению .

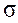Эмпирическая кривая распределения – это фактическая кривая распределения, полученная по данным наблюдения, в которой отражаются как общие, так и случайные условия, определяющие распределение.

Теоретическая кривая распределения – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающем влияние случайных факторов.

Коэффициент асимметрии ( 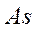) равен отношению центрального момента третьего порядка ( ) к среднему квадратическому отклонению в кубе:

.

Оценка существенности 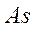проводится на основе средней квадратической ошибки, коэффициента асимметрии , которая зависит от числа наблюдений ( 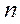) и рассчитывается по формуле: .

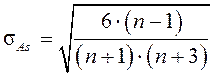Если 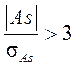асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна и ее наличие может быть вызвано случайными обстоятельствами. Распределение показателя с правосторонней асимметрией приводится к симметричному путем обратного преобразования показателя.

Для симметричных распределений с использованием центрального момент четвертого порядка ( 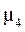) может быть рассчитан показатель эксцесса ( 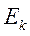), который определяют по формуле: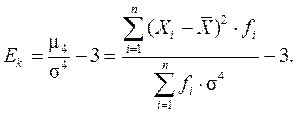

Рис.5. Островершинное ( 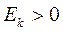, а)) и плосковершинное ( 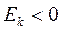, б)) распределения

Среднеквадратическая ошибка эксцесса ( 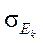) рассчитывается по формуле:

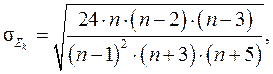где 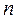- число наблюдений.

Для аппроксимации(выравнивания) эмпирических кривых распределения и сопоставления их с теоретическими в статистике часто пользуются нормальным распределением, функция которого имеет вид:

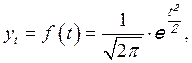
где 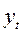- ордината кривой нормального распределения;

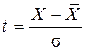- стандартное отклонение;

- варианты вариационного ряда;

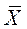- их средняя величина;

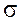- среднее квадратическое отклонение.

Плотность вероятности находится по формуле:

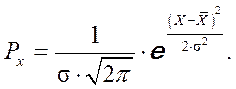
В математической статистике существуют специальные таблицы для любых значений . На основании полученных значений можно найти частоты нормального распределения ( ):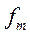

.

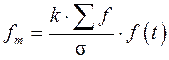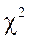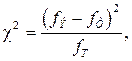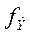Критерии согласия – особые статистические показатели, характеризующие соответствие эмпирического и теоретического распределений. Критерий согласия Пирсона ( ) вычисляется по формуле: где и - эмпирические и теоретические частоты соответственно.