Пропускная способность непрерывного канала связи с шумами
Информация о непрерывном сигнале s(t), получаемая из принимаемой смеси сигнала и шума y(t) = s(t) + n(x)
I(Y, S) = H(Y) – H(Y/S). (2.21)
Так как сигнал и шум статистически независимы, энтропия равна энтропии шума (как случайной величины, сигнал детерминирован и энтропия от него H(S)=0)
H(Y/S) = H(n)
И тогда
I(Y, S) = H(Y) – H(n). (2.22)
Входной сигнал ограничим по полосе пропускания и определим отсчеты по Котельникову (отсчеты независимы и некоррелированы)
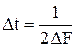 .
.
Количество информации о текущем значении передаваемого сигнала s(t), вносимое дискретным отсчетом принимаемого сигнала y(t), может быть представлено разностью энтропий (приведенных, т.к. процесс непрерывный):
I(Y, S) = H*(Y) – H*(n);
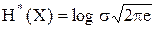 .
.
Отсчеты y(t) = s(t) + n(t) распределены по Гауссу с дисперсией 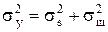 .
.
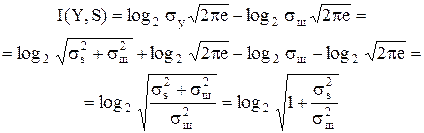 (2.23)
(2.23)
Скорость передачи информации – это количество информации в единицу времени, т.е.
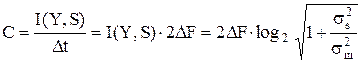 ,
,
т.к. 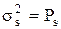 ;
; 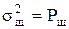 , и окончательно (формула Шеннона):
, и окончательно (формула Шеннона):
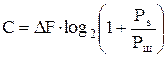 (2.24)
(2.24)
Если Рs/Рш → 0, то С → 0.
Величину (1 + Рs/Рш) – характеризует количество уровней непрерывного сигнала, различимых на фоне шума при данном отношении Рs/Рш. Поэтому количество информации, приходящееся на 1 отсчет, будет в данном случае таким же, как для дискретного источника с числом состояний
(1 + Рs/Рш).
Казалось бы, что можно увеличить скорость передачи информации с увеличением полосы ΔF. Исследуем это предположение.
Преобразуем полученные выражения:
Рш = N0 × ΔF,
тогда
С = ΔF × log2(1 + Рs / N0 × ΔF).
Устремим ΔF → ∞ и раскроем неопределенность
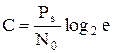 . (2.25)
. (2.25)
Пропускная способность стремится к const.
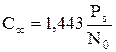 , т.к. log2e = 1,443
, т.к. log2e = 1,443
Скорость передачи информации С стремится к const, определяемой отношением средней мощности сигнала Ps к спектральной плотности шума.
Т.е. обмен мощности сигнала на полосу пропускания для обеспечения заданной пропускной способности непрерывного канала возможен в небольших границах, за которыми дальнейшее расширение полосы пропускания дает уже малый эффект.
Как следует из С∞, для передачи заданного количества информации по каналу с шумом отношение энергии сигнала к спектральной плотности шума h2 = PsT / N0 (I = C × Т – на время сигнала) должно превышать некоторую пороговую величину. В самом деле, если на передачу сообщения затрачено время ΔТ, то среднее количество переданной информации,
I(Y,S) ≤ TC∞, т.к. пропускная способность канала при любой полосе ∆F не может превзойти предельное значение (∆F → ∞). Таким образом,
I(Y,S) ≤ (PsT/N0)log2e и, следовательно, для передачи 1 бита информации необходима энергия сигнала 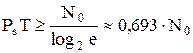 .
.
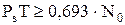 . (2.26)
. (2.26)
Максимальный объем информации, которую можно в среднем передать по непрерывному каналу за время Тк: V = Тк × С, т.е. для Гаусова канала
Vк = Тк × Fк × log2(1 + 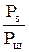 ).
).
Если принять, что Ps/Pш >> 1 и единицей пренебречь
Vк = Тк × Fк × log2( 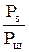 ) = Тк × Fк × Dк. (2.27)
) = Тк × Fк × Dк. (2.27)
где Vк – емкость канала;
D – динамический диапазон (в логарифмах).
Объем сигнала
Vс = Тс × Fс × Dс. (2.28)
Неискаженная передача возможна только при условии
Vс ≤ Vк.
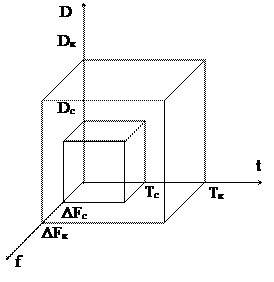 |
Рис. 2.3.
Важно передавать "объем" сигнала, а не его форму. Это дает возможность "трансформировать" объем. Например, уменьшение полосы частот (ΔF) должно приводить к увеличению времени (Тк) для сохранения объема или к увеличению Dк – динамического диапазона, и наоборот.
Сравним пропускные способности дискретного и непрерывного каналов.
Для непрерывного канала:
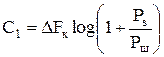
пронормируем по ∆F
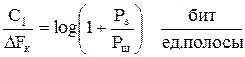 . (2.29)
. (2.29)
Для дискретного канала с шумами:
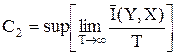
или
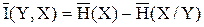
и тогда
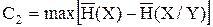 ;
; 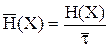 ;
;
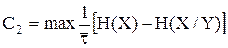 .
.
Для бинарного канала с учетом 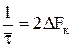 по Котельникову
по Котельникову
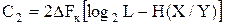 .
.
Для бинарного канала L = 2
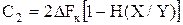 .
.
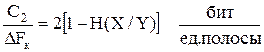 . (2.30)
. (2.30)
Для бинарного сигнала
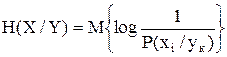
математическое ожидание (осреднение):
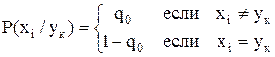 ,
,
q0 – вероятность ошибки P(xi / yк).
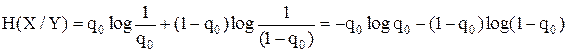
тогда
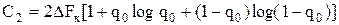 .
.
Пронормируем по ∆F
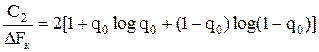 .
.
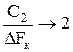 , если q0 → 0 (при
, если q0 → 0 (при 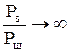 )
)
Если основание не 2, а m, то
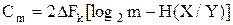
и
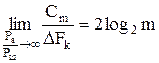 . (2.31)
. (2.31)
 При m → ∞,
При m → ∞, 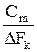 → к непрерывному.
→ к непрерывному.
Рис. 2.4.
Для непрерывного канала монотонно возрастает, для бинарного ограниченно (2 бит), для m-ичного больше.
[1] Понятие усреднения (определение среднего значения), процедура которого обозначается символом М[ ] (см лекцию 1)
Дата добавления: 2016-01-18; просмотров: 1094;
