Энтропия непрерывной случайной величины

В каналах передачи информации часто используются сигналы, мгновенные значения которых могут принимать любые значения на некотором интервале (речевые, музыкальные, телевизионные сигналы и т.д.)

Распространим понятие энтропии на случай непрерывной случайной величины (см. рис. 2.2)

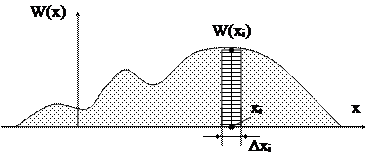Рис. 2.2

Вероятность попадания сигнала в промежуток x…x+dx равна

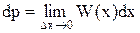
Таким образом:

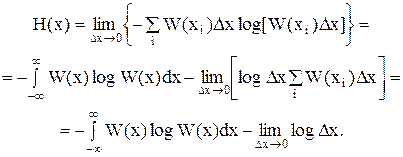(2.11)

Вторая составляющая (2.11) при переходе к пределу превращается
в ∞. Таким образом, энтропия непрерывной случайной величины равна ∞. В связи с этим может возникнуть сомнение в целесообразности энтропийного принципа измерения информации применительно к непрерывно распределенным сигналам. Однако, с теоретической точки зрения эта трудность не является принципиальной. Дело в том, что второе слагаемое выражения (2.11) не зависит от вероятностных характеристик случайной величины, иными словами, второе слагаемое с точностью до бесконечно малой величины одинаково для всех случайных величин. 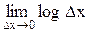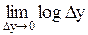Поскольку в реальных каналах всегда имеют место шумы и вычисление информационных характеристик каналов сводится к определению разности энтропии сигнала и шума, в результате вычитания составляющие энтропии вида и взаимно уничтожаются.

При рассмотрении экспериментальных данных дело упрощается еще и тем, что элементы Δх остаются конечными, поскольку эти величины определяются разрешающей способностью измерительных приборов, которая не может быть бесконечной.

Так как при вычислении разности энтропий второе слагаемое выражения (2.11) не представляет интереса, используют только первую составляющую выражения (2.11).

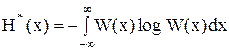, (2.12)

которое называется приведенной или относительной энтропией.

Поскольку выражения для приведенной энтропии непрерывной случайной величины и энтропии дискретной случайной величины аналогичны, очевидно, что приведенная энтропия достигает максимума при равновероятном распределении состояний.

Известно, что при фиксированной дисперсии энтропия максимальна при нормальном законе распределения, т.е. непрерывная случайная величина с фиксированной дисперсией и нормальным распределением обладает максимальной информативностью.

Приведенная энтропия нормально распределенной случайной величины

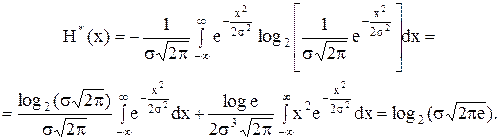(2.13)

Частная и средняя взаимные энтропии непрерывного сигнала

Проделав преобразования, аналогичные тем, которые были проделаны для дискретного сигнала, можно получить следующие выражения для взаимной информации непрерывного сигнала:

1. информация от события к событию

,

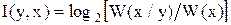2. частная информация

,

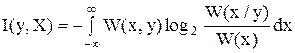3. полная (средняя) информация

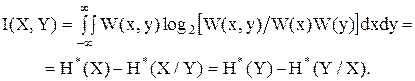
Литература:

[1] стр. 136-138. [2] стр. 245-249. [3] стр. 112-114.

Контрольные вопросы:

1. Почему энтропия непрерывной системы описывается приведенной энтропией?

2. Что такое дифференциальная энтропия?

3. Чем отличается дифференциальная энтропия от обычной энтропии?

4. Как влияет точность отсчета на дифференциальную энтропию?

5. При каком распределении дифференциальная энтропия максимальна для сигналов одинаковой средней мощности?