Пропускная способность канала связи без шумов
Пропускной способностью канала связи называется верхняя грань скорости передачи информации при заданных фиксированных ограничениях:
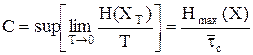 , (2.17)
, (2.17)
где 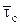 - средняя длина символа.
- средняя длина символа.
Как уже указывалось, Нmax = log2L.
Таким образом,
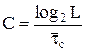 .
.
Для бинарного канала (L = 2) при одинаковой длительности обоих сигналов
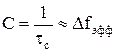 .
.
где Δfэфф – эффективная полоса пропускания канала.
Фундаментальную роль в теории эффективного кодирования играет следующая теорема Шеннона.
Если пропускная способность канала связи больше производительности источника
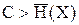 ,
,
то всегда можно закодировать достаточно длинное сообщение так (подобрать такой вид), чтобы оно передавалось каналом связи без задержки. При
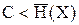 ,
,
передача информации без задержки невозможна.
Не указывая путей построения эффективных кодов, эта теорема определяет предельные возможности эффективного кодирования.
Литература:
[1] стр. 139-141. [2] стр. 235-238. [3] стр. 114-117.
Контрольные вопросы:
1. От чего зависит максимум пропускной способности канала связи?
2. Чем определяется пропускная способность бинарного канала?
3. Когда возникает задержка в передаче информации по каналу связи.
4. Сравните пропускные способности двух дискретных каналов без помех, если в первом канале основание кода m1 = 2, а во втором канале
m2 = 8, и количество символов, передаваемых в секунду, в первом канале V = 100, а во втором V = 40.
Дата добавления: 2016-01-18; просмотров: 854;
