Эффективное (экономное) кодирование
Кодированием называется представление сообщения в виде последовательности символов некоего алфавита.
Кодирование называется экономным (эффективным), если длина кодовых комбинаций – минимальна.
Для эффективного кодирования код должен быть составлен так, чтобы, во-первых, каждый символ нес максимально возможную информацию, т.е. обладал максимальной энтропией, а, во-вторых, элементы сообщения должны кодироваться неравномерным кодом: кодовая информация должна быть тем короче, чем больше частота повторения (вероятность) кодируемого элемента.
Простейшие коды, не учитывающие связи между символами (некоррелированы), есть коды Шеннона-Фано и Хафмена.
Известно, что при отсутствии корреляции между символами скорость передачи информации будет максимальной при условии равной вероятности символов 0 и 1. В соответствии с этим построение кода Шеннона-Фано производится методом дихотомий (последовательное разделение пополам). Все подлежащие кодированию символы разбиваются на две группы так, чтобы суммы вероятностей появления символов в каждой группе были бы по возможности одинаковыми. В результате такого разбиения образовано новое сообщение, состоящее всего из двух элементов, вероятности появления которых одинаковы. Всем символам первой группы приписывается 0, второй – 1 и т.д. Например:
Дано Р(х1) = 0,5; Р(х2) = 0,25; Р(х3) = Р(х4) = 0,125.
Выписываем по порядку уменьшения вероятности:
| Сим-волы | Вероят-ности | Этапы деления | Символы кода | Код Ш-Ф | Двоичный код | ||||
| х1 | 0,5 | I | |||||||
| х2 | 0,25 | II | I | ||||||
| х3 | 0,125 | II | I | ||||||
| х4 | 0,125 | II |
Как видно, полученный код является неравномерным, т.к. длина кодовых комбинаций находится в обратной зависимости от их вероятности. Для любой группы вероятности 0 и 1 одинаковы. Кроме, того, ни одна кодовая комбинация не является началом другой – это необходимо для их разделения.
Максимально возможная скорость передачи бинарного канала, как следует из (2.5) составляет
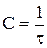 . (2.18)
. (2.18)
Подсчитаем скорость передачи информации, которая обеспечивается полученным кодом.
Пусть длительность символов кода = τ. Тогда средняя длительность кодовых комбинаций:
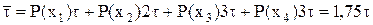 .
.
Средняя энтропия на символ сообщения:
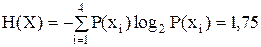 бит/сек.
бит/сек.
Таким образом, скорость передачи информации
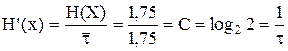 .
.
Следовательно, полученный код позволил получить максимально возможное значение скорости передач информации, т.е. обеспечить полное согласование статистических характеристик источника сообщения со свойствами канала.
При кодировании двоичным равномерным кодом, где каждый символ передается двухразрядной комбинацией, т.е. длительность каждого символа равна 2τ скорость передачи составит:
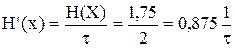 .
.
Таким образом, неэффективный код не полностью использует канал связи, имея большую среднюю длительность передачи каждого символа.
Литература:
[1] стр. 135-136. [3] стр. 109-112.
Контрольные вопросы:
1. Каким должен быть экономный код: равномерным или неравномерным?
2. Применимо ли эффективное кодирование для бинарного источника?
3. Чем определяется пропускная способность бинарного канала связи?
4. Что называется избыточностью алфавитного источника?
Дата добавления: 2016-01-18; просмотров: 1223;
