Процентные ставки и методы их начисления

Известны две основные схемы дискретного начисления:

· схема простых процентов;

· схема сложных процентов.

Схема простых процентов предполагает неизменность базы, с которой происходит начисление:

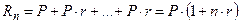
В случае начисления сложных процентов происходит капитализация процентов по мере их начисления, т.е. база, с которой начисляются проценты, все время возрастает. Следовательно, размер инвестированного капитала будет равен:

· к концу первого года: ;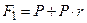

· к концу второго года: ;

· к концу n-го года: .

, при 0<n>1;

, при n>1.

Таким образом, в случае ежегодного начисления процентов для лица, предоставляющего кредит:

· более выгодной является схема простых процентов, если срок ссуды менее одного года, (проценты начисляются однократно в конце периода);

· более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

· обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

Формула сложных процентов является одной из базовых формул в финансовых вычислениях, поэтому для удобства пользования значения множителя FMl(r,n), называемого мультиплицирующим множителем и обеспечивающего наращение стоимости, табулированы для различных значений г и n:

,

где 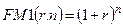- мультиплицирующий множитель.

Экономический смысл множителя FMl(r, n) состоит в следующем: он показывает, чему будет равна одна денежная единица (один рубль, один доллар, одна иена и т.п.) через n периодов при заданной процентной ставке r.