Виды и формы взаимосвязей между явлениями
Все явления общественной жизни находятся во взаимосвязи и взаимообусловленности. Одной из важнейших задач статистики является установление и измерение связи и зависимости между явлениями.
Так как формы и виды этих взаимосвязей весьма разнообразны, существуют их различные классификации.
Прежде всего, необходимо отметить, что по своему содержанию связи между экономическими явлениями могут быть:
- балансовые: они имеют большое распространение в системе национальных счетов, в экономике промышленности, торговли и т.д.
Например:
Стоимость Стоимость Стоимость Стоимость
основных + основных = основных + основных
средств на средств, средств на средств,
начало года поступивших конец года выбывших
за год за год
- компонентные, в которых изменение показателя определяется изменением другого показателя, входящего в его состав.
Например: основные средства = здания + сооружения + передаточные устройства + машины и оборудование + транспорт + инструменты и инвентарь + прочие основные средства.
- причинно-следственные (факторные), в которых изменение одного из факторов (причины) ведёт к изменению другого (следствия).
Например: рост текучести кадров (х) ведет к снижению производительности труда (у).
Причина – признак-фактор (x).
Следствие – признак-результат (y).
Объектом нашего внимания в данном случае и будут факторные или причинно-следственные связи.
По степени тесноты связи (по степени детерминизма) эти связи могут быть двух видов:
- функциональные;
- стохастические (статистические).
Функциональная связь предполагает, что определённому значению признака-фактора соответствует одно, строго определённое значение признака-результата.
Например:
S = πτ2
y = 3,14x2
| x = 1 | у = 3,14 |
| x = 2 | у = 12,56 |
| x = 3 | у = 28,26 |
| x = … | у = … |
| x = 10 | у = 314,00 и т.д. |
Такие связи принято называть жёсткими или полными. Они присутствуют в физике, математике, астрономии и других точных науках.
Статистические связи присущи социально-экономическим явлениям и характеризуются тем, что в данном случае связь наблюдается не в каждом конкретном случае, а в среднем, при большом количестве наблюдений.
Например:
| Стаж работы, лет (x) | % выполнения норм выработки (у) |
| … | … |
То есть, одному и тому значению x = 5 соответствует у = 102 % и у = 104 %; или разным x = 5 и x = 4 соответствует y = 102 %. Это неполная, нежёсткая связь, так как на признак-результат действует много других, кроме учтённого, признаков-факторов. Однако в среднем при увеличении стажа работы увеличивается % выполнения норм выработки.
Частным случаем статистической связи является корреляционная связь.
Связь, которая проявляется при большом числе наблюдений в виде определённой зависимости между средним значением признака-результата и признаком-фактором называется корреляционной.
По числу взаимодействующих факторов связи бывают:
- однофакторные (парная корреляция);
- многофакторные (множественная корреляция).
По направлению эти связи могут быть:
- прямые, когда с увеличением признака-фактора (x) признак-результат (y) также увеличивается;
- обратные, когда с увеличением значений признака-фактора (x) наблюдается уменьшение значений признака-результата (y).
По форме (по аналитическому выражению) статистические связи могут быть:
- линейные (прямолинейные) - величина признака-результата равномерно изменяется под воздействием признака-фактора
y = a0 + a1x ;
- нелинейные (криволинейные), когда величина признака-результата изменяется под воздействием признака-фактора неравномерно:
например, по уравнению параболы y = a0 + a1x + a2x2; показательной функции 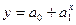 и т.п.
и т.п.
Общая задача статистического изучения взаимосвязей может быть сформулирована следующим образом:
- по результатам n измерений исследуемых факторов x и y
| x1 | x2 | x3 | x4 | … | xn |
| y1 | y2 | y3 | y4 | … | yn |
необходимо получить функцию, которая позволила бы по заданным значениям факторных переменных (x) восстанавливать (прогнозировать) значения результирующих переменных (y), то есть y = f(x).
Однако задачи исследования взаимосвязей могут быть конкретизированы и носить более частный характер в зависимости от цели исследования:
1) выявление наличия или отсутствия корреляционной связи между изучаемыми признаками;
2) измерение тесноты связи между признаками;
3) определение математической модели для описания зависимости между признаками: признаком-результатом и одним либо несколькими признаками-факторами.
Для решения каждой из этих задач теория статистики разработала свои приёмы и методы:
- 1-ая задача может быть решена с помощью так называемых элементарных методов изучения взаимосвязей: графического, балансового, метода аналитических группировок, метода сравнения параллельных рядов;
- 2-ая задача может быть решена с помощью корреляционного анализа, дисперсионного анализа;
- 3-я задача требует построения функции y = f(x), то есть проведения регрессионного анализа.
Дата добавления: 2016-01-16; просмотров: 1650;
