Графический метод (метод корреляционного поля)

Графический метод часто называют методом корреляционного поля. Сущность его заключается в следующем: на график, у которого одна ось х – признак-фактор, а другая ось у – признак-результат, наносятся точки, отображающие исходную информацию (удобнее в ранжированном виде, по таблице 10.2), и соединяются ломаной линией. Далее по расположению этих точек на графике делается вывод о наличии, направлении и, частично, о тесноте связи:

а) если точки на графике концентрируются около некоторой прямой, направленной из левого нижнего в правый верхний угол, то принимается вывод о наличии прямой связи (связь есть, связь прямая);

б) если точки концентрируются около прямой, направленной из левого верхнего в правый нижний угол, связь есть и она обратная;

в) если точка концентрируется в виде дуги около некоторой кривой (например, параболы) принимается вывод о наличии криволинейной связи;

г) если на корреляционном поле наблюдается хаотичный разброс точек, принимается вывод об отсутствии взаимосвязи исследуемых признаков.

Примерный вывод о тесноте связи делается на основании разброса точек на корреляционном поле. Чем ближе они концентрируются вокруг некоторой прямой или кривой, т.е. чем меньше их рассеяние, тем теснее корреляционная связь.

В нашем примере (рисунок 10.1) точки на корреляционном поле концентрируются около прямой, направленной из левого нижнего в правый верхний угол, что позволяет сделать вывод о наличии прямой зависимости между фондоотдачей и удельным весом активной части в общей стоимости основных средств. Более того, точки сконцентрированы достаточно близко к некоторой прямой.

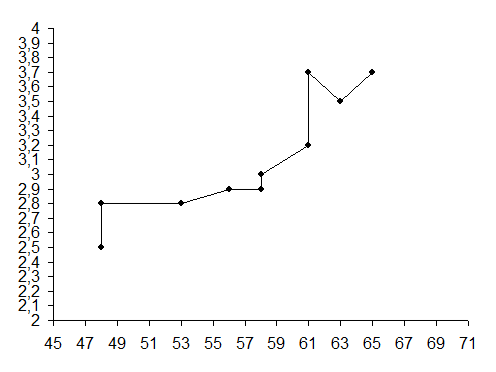
Рисунок 10.1 – Корреляционное поле зависимости фондоотдачи (у) от удельного веса активной части основных средств (x)

Вывод: связь есть, связь прямая и достаточно тесная.

Балансовый метод

Этот метод имеет и целый ряд других названий: табличный метод, метод корреляционной таблицы, метод корреляционной решетки.

Для построения такой таблицы (она имеет форму шахматной таблицы), группируются уровни х и у исходя из следующих правил:

- интервалы устанавливаются равные, т.е. ширина интервала определяется по формуле:

для признака-фактора ,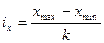

для признака-результата ;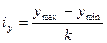

- количество групп (k) одинаковое для х и для у;

- количество интервалов не следует делать большим, т.к. таблица теряет наглядность (хотя строгих правил нет).

В нашем примере примем k = 4, тогда

,

.

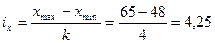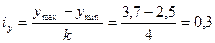После этого строится макет корреляционной таблицы по строкам – признак-фактор, по столбцам – признак-результат.

Группы предприя- тий по y   Группы предприятий по х	2,5 -2,8	2,8-3,1	3,1-3,4	3,4-3,7	Всего
48,00 - 52,25	.	.
52,25 – 56,50		..
56,50 – 60,75		..
60,75 – 65,00			.	…
Всего

Заполнение построенной таблицы производится методом точек или черточек: на пересечении соответствующей строки (х) и столбца (у) в любом месте квадрата (прямоугольника) ставится точка либо черточка. Иногда ставится число, показывающее общее количество единиц совокупности, которое попало в данный прямоугольник (в левом верхнем квадрате должна быть 1, а в правом нижнем – 3).

На последнем этапе производится анализ расположения единиц совокупности по группам, т.е. в таблице:

а) если точки впиваются в эллипс, направленный из левого верхнего в правый нижний угол, связь есть, и она прямая;

б) если точки вписываются в эллипс, направленный из левого нижнего в правый верхний угол, связь есть, и она обратная;

в) если точки концентрируются около некоторой дуги, делается предположение о наличии криволинейной связи;

г) при хаотичном разбросе данных принимается вывод об отсутствии связи между исследуемыми признаками.

В нашем примере точки в корреляционной таблице вписываются в эллипс, направленный из левого верхнего в правый нижний угол, следовательно, между фондоотдачей и удельным весом активной части основных средств существует прямая связь.