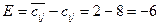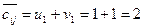Транспортная задача.
Рассмотрим теперь транспортную задачу, непосредственно примыкающую к задаче линейного программирования и хорошо иллюстрирующую общие принципы оптимизации производственных систем [7]. Предположим, на предприятии имеется m складов, которые назовем «поставщиками». На этих складах находится однотипная или взаимозаменяемая продукция, которую потребляют в n цехах.
Количество запасов продукции на каждом складе Ai назовем «мощностью» и обозначим ai (i = 1, 2, …, m). Потребности цехов Bj в заданной продукции будем рассматривать как «спрос» и обозначать bj (j = 1, 2, …, n). Склады находятся от цехов на разных расстояниях. Обозначим эти расстояния через c ij . Количество продукции, перевозимое от каждого склада-поставщика до цеха-потребителя, обозначим через x ij.
С использованием принятых обозначений транспортная задача записывается следующим образом в матричном виде:
| Поставщики Ai и их мощность ai | Потребители Bj и их спрос bj | |||||
| В1 | ……. | Вj | ……. | Вn | ||
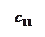 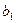
| ……. | 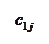 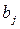
| …….. | 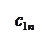 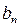
| ||
| A1 |  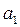
| 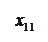
|  …….. ……..
| 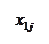
|  …….. ……..
| 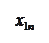
|
| ……. | …….. | …… | ……. | ……. | ……. | …….. |
| Ai |  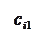 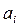
| 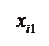
|  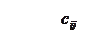 …….. ……..
| 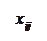
|  …….. ……..
| 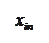 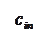
|
| ……. | ..…. | ….. | ……. | ..….. | ……. |  ……… ………
|
| Am |  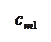 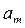
| 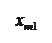
|  …….. ……..
| 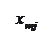 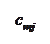
|  ……. …….
| 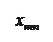 
|
Условия этой задачи заключаются в следующем:
1. Каждый поставщик должен дать потребителям столько продукции, сколько у него есть, т. е.
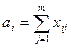 ,
, 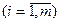 .
.
2. Каждый потребитель должен получить столько продукции, сколько требуется, т. е.
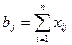 ,
, 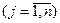 .
.
3. Из первых двух условий вытекает, что сумма мощностей всех поставщиков должна равняться суммарному спросу всех потребителей.
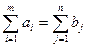 .
.
4. Исходя из этих условий, необходимо найти выгоднейший вариант плана поставок, т. е функция цели F должна быть минимальной:
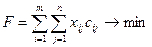 .
.
5. Мощность и спросы должны быть неотрицательны
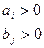 .
.
6. Не должны рассматриваться отрицательные поставки
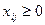 .
.
7. Показатели cij (если это не является бессмысленным) могут принимать отрицательные значения.
Данная задача характеризуется тем, что уравнений в ней меньше, чем неизвестных. Это означает, что в ней имеется множество вариантов плана. Каждый план, который удовлетворяет условиям 1-6, называется допустимым. Решение транспортной задачи начинается с составления базисного плана.
Базисный план должен быть как можно ближе расположенным к оптимальному плану. Существует несколько методов составления базисного плана.
1. Метод Северо-Западного угла.
Это самый простой метод, но при нем получается план, далекий от оптимального плана. Чтобы воспользоваться этим методом необходимо начать заполнять таблицу, начиная от левого верхнего угла и кончая нижним правым углом матрицы (см. приложение 2).
2. Наименьший элемент в столбце (строке). Этот метод заключается в том, что поочередно в столбцах (строках) матрицы заполняются клетки, соответствующие минимальным значениям cij .
Если при записи поставок спрос по столбцу (или мощности по строке) удовлетворен не полностью, ищется следующий по величине элемент в данном столбце (строке) и так до полного удовлетворения спроса. Только после этого переходят на следующий столбец (строку). Если в столбце (строке) имеется два или несколько одинаковых показателей 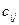 , то может быть принят любой из них для составления плана перевозки.
, то может быть принят любой из них для составления плана перевозки.
3. Наименьший элемент в матрице. В этом случае выбирается наименьший элемент в матрице, а затем наименьший из оставшихся элементов и т. д.
Допустим, мы имеем следующую матрицу поставщиков, потребителей и расстояний с ij между ними (усл. ед.):
 |
 
| 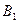
| 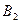
| 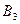
| 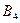
| |
| b 1 = 45 | b 2 = 55 | b 3 = 51 | b 4 = 49 | ||
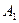
| а 1 = 20 | с 11 = 10 | с 12 = 1 | с 13 = 2 | с 14 = 8 |
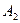
| a 2 = 30 | с 21 = 8 | с 22 = 3 | с 23 = 21 | с 24 =1 |
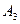
| a 3 = 40 | с 31 =6 | с 32 = 5 | с 33 = 6 | с 34 =4 |
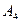
| a 4 = 50 | с 41 =4 | с 42 = 7 | с 43 = 9 | с 44 =6 |
| a 5 = 60 | с 51 =3 | с 52 = 4 | с 53 = 2 | с 54 = 8 |
Составим первый опорный план методом северо-западного угла, т. е. записывая в клетки поставки продукции xij , начиная с левого верхнего угла:
 |
| 
| 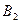
| 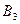
| 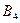
| |
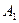
|  
| ||||
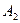
|  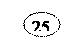
|  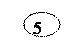
| |||
|  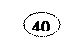
| ||||
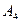
|  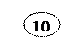
|  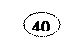
| |||
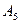
|  
| 
|
Перемножая cij и xij в совпадающих клетках таблицы и складывая, получаем для этого плана функцию цели, равную:
F = 20∙10 + 25∙8 + 5∙3 + 40∙5 + 10∙7 + 40∙9 + 11∙2 + 49∙8 = 1459
Первый опорный план, составленный методом наименьшего элемента в столбце, выглядит следующим образом:
| 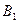
| 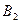
| 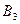
| 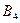
| |
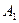
|    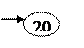
| ||||
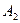
|    
| ||||
|   
| ||||
|  
| 
| |||
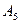
|  
|   
| 
|
Для этого плана функция цели равна:
F = 45∙3 + 20∙1 + 30∙3 + 5∙4 + 40∙6 + 1∙9 + 10∙2 + 49∙6
Первый опорный план, составленный методом наименьшего элемента в таблице, выглядит следующим образом:
| 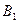
| 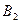
| 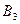
| 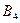
| |
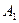
|  
| 
| |||
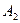
|   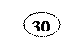
| ||||
|  
|   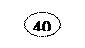
| |||
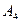
|  
|  
|  
| ||
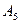
|  
|  
|
Для этого плана функция цели равна: 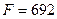 .
.
При составлении первого опорного плана возможен случай вырождения. Он возникает, если при записи поставки мощность окажется равной спросу. В этом случае одновременно из дальнейшего рассмотрения будут исключены строка и столбец. Тогда число неизвестных 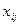 станет меньше числа
станет меньше числа 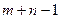 , и нельзя будет проводить оптимизацию. Чтобы избежать вырождения (т. е. если при записи поставки одновременно исчерпывается мощность соответствующего поставщика, и полностью удовлетворен спрос), необходимо сразу же ввести фиктивную (нулевую) поставку по данной строке или столбцу.
, и нельзя будет проводить оптимизацию. Чтобы избежать вырождения (т. е. если при записи поставки одновременно исчерпывается мощность соответствующего поставщика, и полностью удовлетворен спрос), необходимо сразу же ввести фиктивную (нулевую) поставку по данной строке или столбцу.
Как правило, базисный план не является оптимальным. Существует ряд методов получения оптимального плана (окончательного решения транспортной задачи). Рассмотрим решение транспортной задачи методом потенциалов. Потенциалами выступают определенным образом подобранные числа, с помощью которых можно проверить, является ли допустимый план одновременно и оптимальным. Обозначим:
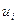 – потенциал строки;
– потенциал строки;
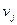 – потенциал столбца;
– потенциал столбца;
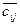 – критерий оптимальности (равный показателю с ij из условий задачи для вошедших в опорный план клеток).
– критерий оптимальности (равный показателю с ij из условий задачи для вошедших в опорный план клеток).
Сумма потенциалов строки и столбца должна быть равно показателю оптимальности 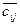 , т. е.
, т. е.
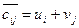 ,
, 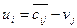 ,
, 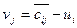 .
.
Рассмотрим технику решения транспортной задачи вручную на конкретном примере. Пусть транспортная задача задана исходной матрицей запасов, потребностей и расстояний между поставщиками и потребителями:
Таблица 5.4.1 Исходная матрица.
 Потребители
Потребители
| 
| 
| 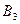
| 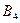
| 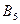
| Мощность запасов |
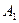
| ||||||
| ||||||
| ||||||
| ||||||
| Потребности Потребителей |
Решение:
1. Составляем первый опорный план, например, используя метод северо-западного угла.
Таблица 5.4.2. Опорный план № 1.
| Поставщики и их мощность | Потребители и их спрос | ||||
| B1 = 80 | B2 = 50 | B3 = 60 | B4 = 20 | B5 = 50 | |
| A1 = 40 |  40 40
| ||||
| A2 = 120 | |||||
| A3 = 60 | |||||
| A4 = 40 |
Для первого плана целевая функция оказывается равной:
F1 = 40×5 + 40×10 + 50×7 + 30×9 + 30×6 + 20×4 + 10×12 + 40×4 = 1760.
2. Определяем потенциалы для первого опорного плана.
 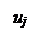 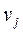
| 4 = 5 – 1 | 1 = 7 – 6 | 3 = 9 – 6 | 1 = 4 - 3 | 9 = 12 – 3 |
| 6 = 10 - 4 | |||||
| 3 = 6 – 3 | |||||
| (-5) = 4 - 9 |
 - значения в клетках переносятся из условий задачи и равны
- значения в клетках переносятся из условий задачи и равны 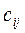 .
.
3. Заполняем все свободные клетки таблицы потенциалов следующим образом:
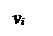  
|
| ||||
2   8 8
  -6 -6
| |||||
| …………. | ………….. | …………… | ………….. |
|
|
Определение: показатель 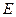 называется характеристикой свободных переменных.
называется характеристикой свободных переменных.
Если величина 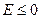 для всех свободных переменных, то исходный план определяет оптимальное решение. Если в некоторых клетках есть значения
для всех свободных переменных, то исходный план определяет оптимальное решение. Если в некоторых клетках есть значения 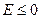 , то можно путем перераспределения поставок улучшить значение функции цели (F). Для этого следует отметить, что перераспределение поставок по цепи к этой клетке уменьшает функционал (в расчете на единицу перераспределяемой продукции) на величину характеристики (E). Теперь вся таблица имеет вид:
, то можно путем перераспределения поставок улучшить значение функции цели (F). Для этого следует отметить, что перераспределение поставок по цепи к этой клетке уменьшает функционал (в расчете на единицу перераспределяемой продукции) на величину характеристики (E). Теперь вся таблица имеет вид:
Таблица 5.4.3
| 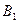
| 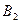
| 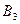
| 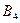
| 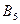
| |
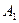
| 2 8 -6 | 4 3 | 2 10 -8 | 10 4 | ||
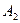
| 7 6 |  15 5 15 5
| ||||
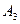
| 7 7 | 4 3 | ||||
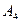
| -5 | -1 6 -7 | -4 3 -7 | -2 11 -13 | -4 5 -9 |
4. Отыскиваем максимальное значение характеристики свободных переменных (E max). В нашем примере она находится в клетке A2-B5 и равна 10 (это значение обведено кружком).
Вводим свободную переменную в клетку A2-B5 (см. опорный план № 1, Табл. 5.4.1). Обозначим ее через 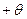 .
.
Таблица 5.4.4 Изменение плана № 1.
| Поставщики и их мощность | Потребители и их спрос | ||||
| B1 = 80 | B2 = 50 | B3 = 60 | B4 = 20 | B5 = 50 | |
| A1 = 40 | |||||
| A2 = 120 |  30 - 30 - 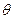
| + 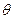 . .
| |||
| A3 = 60 | 30 + 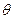
| 10 - 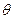 . .
| |||
| A4 = 40 |
Правило 1: Абсолютная величина поставки 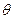 должна быть в точности равна величине возможных ликвидируемых поставок. В нашем случае она равна:
должна быть в точности равна величине возможных ликвидируемых поставок. В нашем случае она равна: 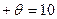 .
.
Правило 2: Баланс поставок по столбцам и строкам не должен нарушаться.
В нашем примере из-за введения свободной переменной 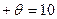 нарушен баланс в столбце B5 и строке A2 (см. свободную переменную в клетку . Чтобы сохранить его, вводим в A2-B3 свободную переменную
нарушен баланс в столбце B5 и строке A2 (см. свободную переменную в клетку . Чтобы сохранить его, вводим в A2-B3 свободную переменную 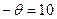 .
.
Баланс по строке A2 этим самым восстановлен, но нарушен баланс во столбцу B3. Восстанавливая его, в A3-B3 введем 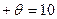 , и в A3-B5 переменную
, и в A3-B5 переменную 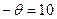 . Эта процедура носит название построение цепей. Очевидно, что цепи должны быть замкнуты.
. Эта процедура носит название построение цепей. Очевидно, что цепи должны быть замкнуты.
5. Составляем план перевозок № 2.
Таблица 5.4.5
| B1 | B2 | B3 | B4 | B5 | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 |
Получаем F2 = 1660, что на 100 единиц меньше, чем в первом плане. Для каждой итерации приращение функции цели всегда равно 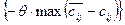 .
.
Вновь составляем таблицу потенциалов, далее составляем новый план, и т. д. Эта процедура повторяется вновь и вновь до тех пор, пока не получится устойчивое решение. Для окончательного решения рассматриваемой задачи достаточно составить всего 8 планов перевозок. В итоге получаем следующее оптимальное решение: F8 = 1430 = min. При этом оптимальный план перевозок № 8 имеет вид:
Таблица 5.4.6
| B1 | B2 | B3 | B4 | B5 | |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| A4 |
Если мы имеем дело с открытой транспортной задачей, то путем введения фиктивной мощности или фиктивного спроса можно привести её к виду закрытой транспортной задачи, причем величины 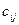 для фиктивных параметров все равны нулю.
для фиктивных параметров все равны нулю.
Дата добавления: 2016-01-11; просмотров: 1437;

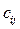 из условий
задачи (табл. 5.4.1)
из условий
задачи (табл. 5.4.1)